《2025年考前示范卷九年级数学全一册人教版》

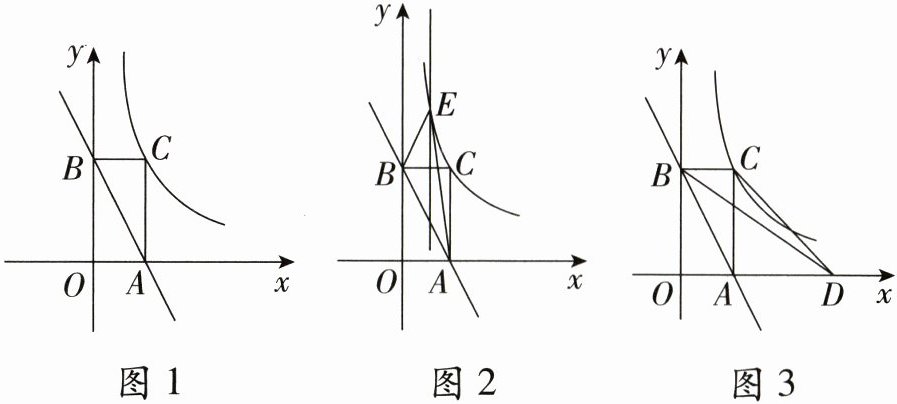
22.(10分)如图1,一次函数y=kx+b的图象与x轴,y轴分别交于点A(1,0)和点B(0,2),以AB为对角线作矩形OACB,点C恰好在反比例函数y=$\frac{m}{x}$(x＞0)的图象上。
(1)求一次函数和反比例函数的表达式;
(2)如图2,作线段BC的垂直平分线,交反比例函数图象于点E,连接AE,BE,求△ABE的面积;
(3)如图3,若D是x轴上一点,则△BCD周长的最小值为________。
　　　　　　　　　　　　　　　　　　

答案：
解:
(1)将点A(1,0)和点B(0,2)代入一次函数表达式y = kx + b，
得$\begin{cases}k + b = 0\\b = 2\end{cases}$，解得$\begin{cases}k = -2\\b = 2\end{cases}$。
∴一次函数的表达式为y = -2x + 2。
∵点A(1,0)，B(0,2)，
∴OA = 1，OB = 2。
∵四边形OACB是矩形，
∴AC = OB = 2。
∴点C(1,2)。
∵点C在反比例函数图象上，
∴m = 2。
∴反比例函数的表达式为y = $\frac{2}{x}$。
∴一次函数的表达式为y = -2x + 2，反比例函数的表达式为y = $\frac{2}{x}$。
(2)由题意，知点E($\frac{1}{2}$,4)，
所以$S_{\triangle ABE}$ = $\frac{1}{2}$×3×1 = $\frac{3}{2}$。
(3)如图，作点B关于x轴的对称点B'，连接CB'交x轴于点D'。
∴点D在点D'的位置时，BD + CD的值最小。

∵点B(0,2)，
∴点B'(0,-2)。
∴$B'C$ = $\sqrt{1² + 4²}$ = $\sqrt{17}$。
∴BD + CD的最小值为$\sqrt{17}$。
∵△BCD的周长为BD + CD + BC，
∴△BCD周长的最小值为$\sqrt{17}$ + $\sqrt{5}$。

23.(12分)数学上的对称通常是指轴对称、中心对称,以及对称的思想方法。某数学兴趣小组进行折纸活动,来感受图形中的对称思想。如图1,将正方形纸片ABCD对折后展开,得到折痕HG;如图2,将纸片再次折叠,使点A落在折痕HG上,记作点F;如图3,连接AF,得到△ABF。
　　　　　　　　　　　
(1)请判断:△ABF是________三角形;
[问题提出]
兴趣小组成员想要进一步找到正方形中最大的等边三角形。
[问题探究]
如图4,小颖认为正方形中最大的等边三角形的顶点一定落在正方形的边上,她将图4的△PRQ 沿AB进行平移,使点Q与点B重合(如图5),再将△PRB绕点B旋转,使PR与对角线BD垂直,延长BR,BP分别交CD,AD于点E,F(如图6),连接EF,便可得到如图7的最大等边三角形。设∠EBF = 15°,则利用正方形ABCD的对称性可求得∠ABF = $\frac{90° - ∠EBF}{2}$。
BF = ________;(sin15° = $\frac{\sqrt{6}-\sqrt{2}}{4}$,cos15° = $\frac{\sqrt{6}+\sqrt{2}}{4}$,tan15° = 2 - $\sqrt{3}$)
　　　　　　
(3)若不知道15°角的三角函数值,请你换一种方法求BF的长;
[问题解决]
(4)已知正六边形中最大的等边三角形的边长为4,则该正六边形的边长为________;
(5)A4纸的长为29.7cm,宽为21cm,现要在A4纸中剪一个最大的等边三角形。请你在图9中画出示意图(不需尺规作图),并求该最大的等边三角形的边长。

答案：
解:
(1)由折叠，知BG = AB = $\frac{1}{2}$BF，∠FGB = ∠FGA = 90°，
∴∠BFG = 30° = ∠AFG。
∴∠AFB = 60°。
又
∵AB = BF，
∴△ABF是等边三角形。
故答案为等边。
(2)在Rt△ABF中，cos∠ABF = $\frac{AB}{BF}$。
∴cos15° = $\frac{\sqrt{6} + \sqrt{2}}{4}$ = $\frac{2}{BF}$。
解得BF = $2\sqrt{6} - 2\sqrt{2}$。
故答案为$2\sqrt{6} - 2\sqrt{2}$。
(3)
∵△BEF关于直线BD对称，
∴DE = DF，△DEF是等腰直角三角形。
设DE = DF = x，则EF = $\sqrt{2}x$ = BF = BE，AF = AD - DF = 2 - x。
在Rt△ABF中，AF² + AB² = BF²。
∴(2 - x)² + 2² = ($\sqrt{2}x$)²。
解得x = $2\sqrt{3} - 2$或 -$2\sqrt{3} - 2$(不符合题意，舍去)。
∴BF = $\sqrt{2}x$ = $\sqrt{2}$×($2\sqrt{3} - 2$) = $2\sqrt{6} - 2\sqrt{2}$。
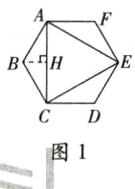
(4)如图1，△ACE是正六边形ABCDEF中边长最大的等边三角形，过点B作BH⊥AC于点H。
∵∠BAF = $\frac{(6 - 2)×180°}{6}$ = 120°，
∴由对称性可得∠BAC = ∠FAE = $\frac{∠BAF - ∠CAE}{2}$ = 30°。
∵BH⊥AC，AB = BC，
∴AH = CH = $\frac{1}{2}$AC = 2，∠AHB = 90°。
在Rt△ABH中，cos∠BAC = $\frac{AH}{AB}$，
∴cos30° = $\frac{\sqrt{3}}{2}$ = $\frac{2}{AB}$。
解得AB = $\frac{4\sqrt{3}}{3}$。
∴正六边形的边长为$\frac{4\sqrt{3}}{3}$。
故答案为$\frac{4\sqrt{3}}{3}$。


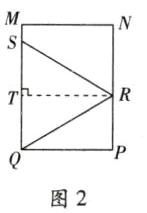
点R如作图，Rt△MQR，RQ⊥MQ于点Q，T即为所求。
∵∠RTQ = ∠TQP = ∠P = 90°，
∴四边形RTQP是矩形。
∴TR = PQ = 21cm。
∵SR = QR，RT = MQ，
∴∠SRT = ∠QRT = 30°。
在Rt△RST中，cos∠SRT = $\frac{TR}{SR}$。
∴cos30° = $\frac{\sqrt{3}}{2}$ = $\frac{21}{SR}$。
解得SR = $14\sqrt{3}$。
∴最大的等边三角形的边长是$14\sqrt{3}$cm。