2025年考前示范卷九年级数学全一册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年考前示范卷九年级数学全一册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
21.(6分)在第19届杭州亚运会上,中国女篮在最后时刻,由王思雨完成绝杀,以74比72的比分险胜日本队,成功卫冕亚运会冠军。如图,在球场上,一名身高1.95米的运动员,垂直起跳高度为0.35米,篮球在头顶上方0.25米的点A处出手,然后准确落入篮框中心点C。篮球(看成点)的运动路径为抛物线的一部分,已知篮框中心到地面的距离为3.05米,当球飞行到离地面最大高度为3.45米的点B时,球与篮框中心的水平距离为2米。
(1)篮球出手处距离地面的高度是________米;
(2)请在图中建立适当的平面直角坐标系,求出篮球出手处到篮框中心的水平距离。
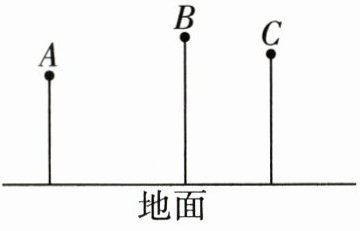
(1)篮球出手处距离地面的高度是________米;
(2)请在图中建立适当的平面直角坐标系,求出篮球出手处到篮框中心的水平距离。

答案:
解:
(1)篮球出手处距离地面的高度为h=1.95+0.25+0.35=2.55(米)。
故答案为2.55。
(2)如图,过点B作水平线的垂线,垂足为0,以点0为坐标原点,直线OB为y轴,建立如图所示的平面直角坐标系。由题意,得该抛物顶点坐标为点B(0,3.45),且过点C(2,3.05)。
设抛物线的表达式为
y=ax²+3.45。
把点C(2,3.05)代入抛
 物线的表达式,
物线的表达式,
得3.05=4a+3.45。
解得a=−0.1。
抛物线的表达式为y=−0.1x²+3.45。
(马,蛇)(,蛇)II点将解得2y得.A=5x251.在==55−3第0,代x.321人=x)²抛−+)33物o。.,4线5。的表达式,
(马,蛇)(,蛇)II点A在第3))o 篮球出手处到篮框中心的水平距离是1xA1+c=.³+2=5(米)。
解:
(1)篮球出手处距离地面的高度为h=1.95+0.25+0.35=2.55(米)。
故答案为2.55。
(2)如图,过点B作水平线的垂线,垂足为0,以点0为坐标原点,直线OB为y轴,建立如图所示的平面直角坐标系。由题意,得该抛物顶点坐标为点B(0,3.45),且过点C(2,3.05)。
设抛物线的表达式为
y=ax²+3.45。
把点C(2,3.05)代入抛
 物线的表达式,
物线的表达式,得3.05=4a+3.45。
解得a=−0.1。
抛物线的表达式为y=−0.1x²+3.45。
(马,蛇)(,蛇)II点将解得2y得.A=5x251.在==55−3第0,代x.321人=x)²抛−+)33物o。.,4线5。的表达式,
(马,蛇)(,蛇)II点A在第3))o 篮球出手处到篮框中心的水平距离是1xA1+c=.³+2=5(米)。
22.(8分)如图,已知一次函数y₁ = mx + n的图象与x轴,y轴分别交于点A,B,与反比例函数y₂ = $\frac{k}{x}$的图象分别交于点C,D,点C的坐标为(−4,1),A是线段BC的中点。
(1)求一次函数与反比例函数的表达式;
(2)求△COD的面积;
(3)直接写出当y₁≥y₂时,自变量x的取值范围。
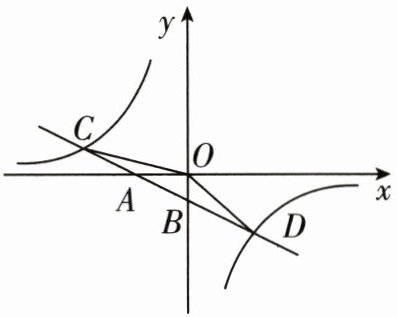
(1)求一次函数与反比例函数的表达式;
(2)求△COD的面积;
(3)直接写出当y₁≥y₂时,自变量x的取值范围。

答案:
解: )将点C的坐标(−4,1)代人反比例函数的表达式y2$\frac{k}{x}$,
习54=。解得k=−4。
∴反比例函数的表达式为y2=−$\frac{4}{x}$。
∵A是线段BC的中点,点B的横坐标为0,点A 的纵坐标为0,点C的坐标为(−4,1),
∴点B的坐标为(0,−1),点A的坐标为(−2,0)。
将B(0,−1),C(−4,1)两点代人一次函数表达式y1=mx+n,
得{n−4=m−+1n,=1。解得m=$\frac{1}{2}$,
n=−1。
∴一次函数表达式为y=−x1−1。
(2)
∵点B的坐标为(0,−1),
∴OB=1。
联立一次函数表达式与反比例函数表达式,得yy==$\frac{4}{x}$−²x。|1,解得==−22,,或{xy==−14。,
∵点D在第四象限内,
∴点D的坐标为(2,−2)。
又
∵点C(−4,1),
∴S△coD=O2 B(xD−xc)=$\frac{1}{2}$x1×(2+4)=3。
(3)观察图象,当y≥y时,自变量x的取值范围是x≤−4或0<x≤2。
习54=。解得k=−4。
∴反比例函数的表达式为y2=−$\frac{4}{x}$。
∵A是线段BC的中点,点B的横坐标为0,点A 的纵坐标为0,点C的坐标为(−4,1),
∴点B的坐标为(0,−1),点A的坐标为(−2,0)。
将B(0,−1),C(−4,1)两点代人一次函数表达式y1=mx+n,
得{n−4=m−+1n,=1。解得m=$\frac{1}{2}$,
n=−1。
∴一次函数表达式为y=−x1−1。
(2)
∵点B的坐标为(0,−1),
∴OB=1。
联立一次函数表达式与反比例函数表达式,得yy==$\frac{4}{x}$−²x。|1,解得==−22,,或{xy==−14。,
∵点D在第四象限内,
∴点D的坐标为(2,−2)。
又
∵点C(−4,1),
∴S△coD=O2 B(xD−xc)=$\frac{1}{2}$x1×(2+4)=3。
(3)观察图象,当y≥y时,自变量x的取值范围是x≤−4或0<x≤2。
23.(8分)如图,在等腰三角形ABC中,AB = BC,BO平分∠ABC,过点A作AD//BC交BO的延长线于点D,连接CD,过点D作DE⊥BD交BC的延长线于点E。
(1)判断四边形ABCD的形状,并说明理由;
(2)若AB = 3,∠ABE = 120°,求DE的长。
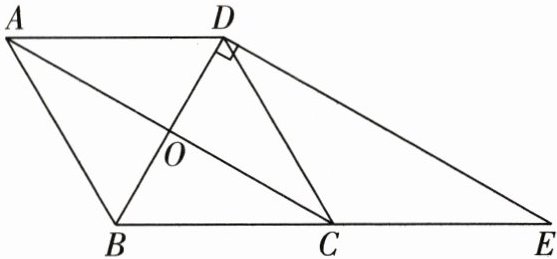
(1)判断四边形ABCD的形状,并说明理由;
(2)若AB = 3,∠ABE = 120°,求DE的长。

答案:
解:
(1)四边形ABCD是菱形。理由如下:
∵AB=BC,BO平分∠ABC,
∴Ao=CO。
∵AD//BE,
∴∠DAO=∠BCO,∠ADO=∠CBO。
∴△ADO△CBO(AAS)。
∴DO=BO。
∴四边形ABCD是平行四边形。
∵AB=BC,
∴四边形ABCD是菱形。
(2)
∵BO平分∠ABC,∠ABE=120°,
∴∠DBC=$\frac{1}{2}$∠ABE=60°。
∵四边形ABCD是菱形,
∴BC=CD=AB=3。
∴△BCD是等边三角形。
∴BD=BC=3。
在Rt△BDE中,
∵BD⊥DE,
∴∠BDE=90°。
∴ E=90°−∠DBE=90°−60°=30°。
∴BE=2BD=6。
∴DE= $\sqrt{BE²−BD²}$=
∴DE的长为3√3。
(1)四边形ABCD是菱形。理由如下:
∵AB=BC,BO平分∠ABC,
∴Ao=CO。
∵AD//BE,
∴∠DAO=∠BCO,∠ADO=∠CBO。
∴△ADO△CBO(AAS)。
∴DO=BO。
∴四边形ABCD是平行四边形。
∵AB=BC,
∴四边形ABCD是菱形。
(2)
∵BO平分∠ABC,∠ABE=120°,
∴∠DBC=$\frac{1}{2}$∠ABE=60°。
∵四边形ABCD是菱形,
∴BC=CD=AB=3。
∴△BCD是等边三角形。
∴BD=BC=3。
在Rt△BDE中,
∵BD⊥DE,
∴∠BDE=90°。
∴ E=90°−∠DBE=90°−60°=30°。
∴BE=2BD=6。
∴DE= $\sqrt{BE²−BD²}$=
∴DE的长为3√3。
查看更多完整答案,请扫码查看


