2025年考前示范卷九年级数学全一册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年考前示范卷九年级数学全一册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
21. (10 分)如图,在 Rt△ABC 中,∠ACB = 90°,过点 C 作直线 MN//AB,D 为 AB 边上一点,过点 D 作 DE⊥BC,垂足为 F,交直线 MN 于 E,连接 CD,BE。
(1)求证:CE = AD;
(2)当 D 为 AB 的中点时,四边形 BECD 是什么特殊四边形?说明你的理由;
(3)在满足(2)的条件下,当△ABC 满足条件________时,四边形 BECD 是正方形。(填空即可,不必说明理由)
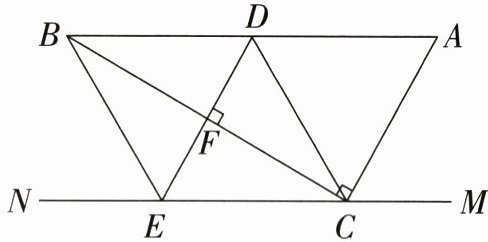
(1)求证:CE = AD;
(2)当 D 为 AB 的中点时,四边形 BECD 是什么特殊四边形?说明你的理由;
(3)在满足(2)的条件下,当△ABC 满足条件________时,四边形 BECD 是正方形。(填空即可,不必说明理由)

答案:
(1)证明:
∵$DE⊥BC$,
∴$∠DFB = 90°$。
∵$∠ACB = 90°$,
∴$∠ACB = ∠DFB$。
∴$AC// DE$。
∵$CE// AD$,
∴四边形ADEC是平行四边形。
∴$CE = AD$。
(2)解:四边形BECD是菱形。理由如下:
∵D为AB的中点,
∴$AD = BD$。
∵$CE = AD$,
∴$BD = CE$。
∵$BD// CE$,
∴四边形BECD是平行四边形。
∵$∠ACB = 90°$,D为AB的中点,
∴$CD = \frac{1}{2}AB = BD$。
∴四边形BECD是菱形。
(3)解:当$△ABC$满足条件$AC = BC$时,四边形BECD是正方形。
∵$∠ACB = 90°$,$AC = BC$,D为AB的中点,
∴$CD⊥AB$。
∴$∠CDB = 90°$。
∴四边形BECD是正方形。
故答案为$AC = BC$。
(1)证明:
∵$DE⊥BC$,
∴$∠DFB = 90°$。
∵$∠ACB = 90°$,
∴$∠ACB = ∠DFB$。
∴$AC// DE$。
∵$CE// AD$,
∴四边形ADEC是平行四边形。
∴$CE = AD$。
(2)解:四边形BECD是菱形。理由如下:
∵D为AB的中点,
∴$AD = BD$。
∵$CE = AD$,
∴$BD = CE$。
∵$BD// CE$,
∴四边形BECD是平行四边形。
∵$∠ACB = 90°$,D为AB的中点,
∴$CD = \frac{1}{2}AB = BD$。
∴四边形BECD是菱形。
(3)解:当$△ABC$满足条件$AC = BC$时,四边形BECD是正方形。
∵$∠ACB = 90°$,$AC = BC$,D为AB的中点,
∴$CD⊥AB$。
∴$∠CDB = 90°$。
∴四边形BECD是正方形。
故答案为$AC = BC$。
22. (12 分)消毒洗手液与百姓生活息息相关,某药店的消毒洗手液很畅销,已知该消毒洗手液的进价为每瓶 20 元,经市场调查,每天洗手液的销售量 y(瓶)与销售单价 x(元)之间满足一次函数关系,部分数据记录如下表:

(1)直接写出 y 与 x 之间的函数表达式;(不需要写自变量 x 的取值范围)
(2)若该药店每天想从这批消毒洗手液的销售中获利 375 元,又想尽量给顾客实惠,问:这批消毒洗手液每瓶的售价为多少元?
(3)该药店上级主管部门规定,消毒洗手液的每瓶利润不允许高于进价的 30%,设这种消毒洗手液每天的总利润为 w(元),那么售价定为多少元时,该药店可获得的利润最大?最大利润是多少元?

(1)直接写出 y 与 x 之间的函数表达式;(不需要写自变量 x 的取值范围)
(2)若该药店每天想从这批消毒洗手液的销售中获利 375 元,又想尽量给顾客实惠,问:这批消毒洗手液每瓶的售价为多少元?
(3)该药店上级主管部门规定,消毒洗手液的每瓶利润不允许高于进价的 30%,设这种消毒洗手液每天的总利润为 w(元),那么售价定为多少元时,该药店可获得的利润最大?最大利润是多少元?
答案:
解:
(1)设$y$与$x$之间的函数表达式为$y = kx + b (k≠0)$。
将$x = 22$,$y = 90$;$x = 24$,$y = 80$分别代入,
得$\begin{cases}22k + b = 90 \\ 24k + b = 80\end{cases}$,解得$\begin{cases}k = -5 \\ b = 200\end{cases}$。
所以$y$与$x$之间的函数表达式为$y = -5x + 200$。
(2)由
(1)知,若每瓶售价为$x$元,每天销售量为$y$瓶。
由题意,得$(x - 20)y = 375$。
∵$y = -5x + 200$,
∴$(x - 20)(-5x + 200) = 375$。
整理,得$x^2 - 60x + 875 = 0$。
解得$x_1 = 25$,$x_2 = 35$。
∵需要尽量给顾客实惠,
∴$x = 25$。
∴这批消毒洗手液每瓶的售价为25元。
(3)由题意,得$w = (x - 20)(-5x + 200)$
$= -5x^2 + 300x - 4000$
$= -5(x - 30)^2 + 500$。
∵消毒洗手液每瓶利润不允许高于进价的30%,
∴$x - 20\leq20×30\%$,解得$x\leq26$。
∵$-5 < 0$,
∴抛物线开口向下。
∴当$x < 30$时,$w$的值随$x$值的增大而增大。
∴当$x = 26$时,总利润$w$最大,
此时$w = -5×(26 - 30)^2 + 500 = 420$(元)。
∴当售价定为26元时,该药店可获得的利润最大,最大利润是420元。
(1)设$y$与$x$之间的函数表达式为$y = kx + b (k≠0)$。
将$x = 22$,$y = 90$;$x = 24$,$y = 80$分别代入,
得$\begin{cases}22k + b = 90 \\ 24k + b = 80\end{cases}$,解得$\begin{cases}k = -5 \\ b = 200\end{cases}$。
所以$y$与$x$之间的函数表达式为$y = -5x + 200$。
(2)由
(1)知,若每瓶售价为$x$元,每天销售量为$y$瓶。
由题意,得$(x - 20)y = 375$。
∵$y = -5x + 200$,
∴$(x - 20)(-5x + 200) = 375$。
整理,得$x^2 - 60x + 875 = 0$。
解得$x_1 = 25$,$x_2 = 35$。
∵需要尽量给顾客实惠,
∴$x = 25$。
∴这批消毒洗手液每瓶的售价为25元。
(3)由题意,得$w = (x - 20)(-5x + 200)$
$= -5x^2 + 300x - 4000$
$= -5(x - 30)^2 + 500$。
∵消毒洗手液每瓶利润不允许高于进价的30%,
∴$x - 20\leq20×30\%$,解得$x\leq26$。
∵$-5 < 0$,
∴抛物线开口向下。
∴当$x < 30$时,$w$的值随$x$值的增大而增大。
∴当$x = 26$时,总利润$w$最大,
此时$w = -5×(26 - 30)^2 + 500 = 420$(元)。
∴当售价定为26元时,该药店可获得的利润最大,最大利润是420元。
查看更多完整答案,请扫码查看


