《2025年考前示范卷九年级数学全一册人教版》

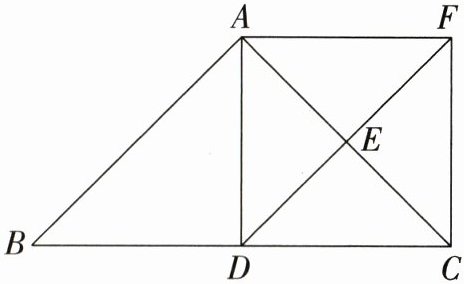
21. (9分)如图,在△ABC中,D,E分别是BC,AC边上的点,F为DE延长线上的点,连接AF,CF。
(1) ① AC平分∠DAF;② AF//DC;③ E是AC的中点;④ DF⊥AC。
请从以上四项中,选择三项作为已知条件,剩余的一项作为结论,形成一个真命题。
把相应序号填写到已知、求证的横线上,并完成证明;
已知:________;求证:________;
(2) 在(1)的情形中,当AB = AC,且AD平分∠BAC时,四边形ADCF是什么特殊四边形？请证明你的结论。

答案： 解:
(1)已知①AC平分∠DAF,②AF//DC,③E是AC的中点;
求证:④DF⊥AC;
证明:
∵AC平分∠DAF,
∴∠FAC = ∠DAC。
∵AF//DC,
∴∠FAC = ∠ACD。
∴∠ACD = ∠DAC。
∴DC = DA。
∵E是AC的中点，
∴DE⊥AC,即DF⊥AC。
故答案为①②③,④。
(2)四边形ADCF是正方形。
证明:
∵AB = AC,AD平分∠BAC,
∴CD = DB,AD⊥BC。
∵E是AC的中点，
∴CE = EA。
∴DE = $\frac{1}{2}$AB，DE//AB。
∵AF//DC,
∴四边形ABDF为平行四边形。
∴AF = BD。
∵CD = DB,
∴AF = CD。
∴四边形ADCF为平行四边形。
∵DF⊥AC,
∴四边形ADCF为菱形。
∵AD⊥BC,
∴四边形ADCF为正方形。

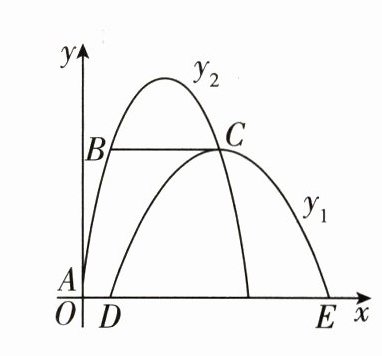
22. (9分)某数学兴趣小组进行项目式学习成果的展示,给出如下信息:在学校的巨幅宣传墙上,勤于动脑的小丽发现两条熟悉的抛物线,她依据环境,建立如图所示的平面直角坐标系,利用手边的工具,她不仅与同学合作进行力所能及的测量,还看到抛物线y₂上的两点B,C组成的线段恰好与学校的一处露台等高,于是通过采访总务处老师获得重要数据,他们发现:抛物线y₁的顶点C的纵坐标为40,y₁与x轴相交于点D(5,0),E(45,0)。抛物线y₂刚好过y₁的顶点C,且与y轴相交于点A(0,2.5),平行于x轴的线段BC长为20。根据以上信息,请你解决如下问题。
(1) 求两条抛物线y₁与y₂的函数表达式;
(2) 当5 ≤ x ≤ 25时,求抛物线y₁与y₂的最大间距。

答案： 解:
(1)由题意，得抛物线y₁的对称轴是直线x = $\frac{5 + 45}{2}$ = 25。
又
∵抛物线y₁的顶点C的纵坐标为40，
∴点C(25,40)。
∴设抛物线y₁的函数表达式为y₁ = a(x - 25)² + 40(a≠0)。
又
∵抛物线y₁过点D(5,0)，
∴400a + 40 = 0。
∴a = - $\frac{1}{10}$。
∴抛物线y₁的函数表达式为y₁ = - $\frac{1}{10}$(x - 25)² + 40。
∵点C(25,40),BC = 20,BC//x轴,
∴点B(5,40)。
∴抛物线y₂的对称轴是直线x = $\frac{5 + 25}{2}$ = 15。
∴设抛物线y₂的函数表达式为y₂ = b(x - 15)² + k(b≠0)。
又
∵抛物线y₂过点A(0,2.5),C(25,40)，
∴$\begin{cases}225b + k = 40\\25b + k = 2.5\end{cases}$，
解得b = $\frac{3}{20}$，k = - $\frac{5}{4}$。
∴抛物线y₂的函数表达式为y₂ = $\frac{3}{20}$(x - 15)² - $\frac{5}{4}$。
(2)当5≤x≤25时，取x = m。
∴y₂ - y₁ = $\frac{3}{20}$(m - 15)² - $\frac{5}{4}$ - [- $\frac{1}{10}$(m - 25)² + 40]
= $\frac{3}{20}$(m² - 30m + 225) - $\frac{5}{4}$ + $\frac{1}{10}$(m² - 50m + 625) - 40
= $\frac{3}{20}m² - \frac{9}{2}m + \frac{135}{4} - \frac{5}{4} + \frac{1}{10}m² - 5m + \frac{125}{2} - 40$
= $\frac{1}{4}m² - \frac{19}{2}m + \frac{130}{4} + \frac{250}{4} - \frac{160}{4}$
= $\frac{1}{4}m² - \frac{19}{2}m + \frac{220}{4}$
= $\frac{1}{4}(m² - 38m + 220)$
= $\frac{1}{4}[(m - 19)² - 361 + 220]$
= $\frac{1}{4}[(m - 19)² - 141]$
又
∵5≤m≤25，
∴当m = 19时，y₂ - y₁的值最大，最大值为$\frac{1}{4}×(- 141 + 141) = 0$。
∴当5≤x≤25时，抛物线y₁与y₂的最大间距为0。