《2025年考前示范卷九年级数学全一册人教版》

23.(8分)在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF//BC交CE的延长线于点F,连接BF。
　(1)求证:四边形ADBF是菱形;
　(2)若AB=8,菱形ADBF的面积为40。求AC的长。
　　

答案：
解:
(1)证明:
∵E是AD的中点，
∴AE=DE。
∵AF//BC,
∴∠AFE=∠DCE
　在△AEF和△DEC中,
　　∠AFE=∠DCE,
　　∠AEF=∠DEC,
　　AE=DE,
∴△AEF≌△DEC(AAS)。
∴AF=DC。
∵D是BC的中点，
∴CD=BD。
∴AF=BD。
∴四边形ADBF是平行四边形。
∵∠BAC=90°,D是BC的中点，
∴AD=BD=$\frac{1}{2}$BC。
∴四边形ADBF是菱形。
(2)如图,连接DF交AB于点O。
　　　　　
由
(1),知四边形ADBF是菱形。
　
　
∴AB⊥DF,OD=$\frac{1}{2}$DF,OA=$\frac{1}{2}$AB=$\frac{1}{2}$×8=4,S菱形ADBF=$\frac{1}{2}$AB·DF=40。
　
∴$\frac{1}{2}$DF×8=40。
　
∴DF=10。
∴OD=$\frac{1}{2}$DF=5。
∵四边形ADBF是菱形，
　
∴O是AB的中点。
　
∵D是BC的中点，
　
∴OD是△ABC的中位线。
　
∴AC=2OD=2×5=10。
　
∴AC的长为10。

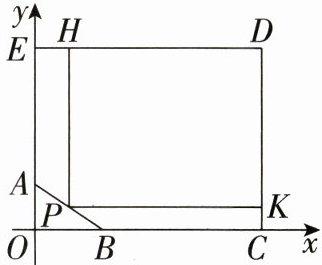
24.(8分)如图,为了绿化小区,某物业公司要在形如五边形的草坪ABCDE上建一个矩形花坛PKDH。已知PH//AE,PK//BC,DE=100m,AE=60m,BC=70m,CD=80m。以BC所在直线为x轴,AE所在直线为y轴,建立平面直角坐标系,坐标原点为0。
　(1)求直线AB的表达式;
　(2)若设点P的横坐标为x,矩形PKDH的面积为S。
　①写出S与x之间的函数表达式;
　②当x为何值时,S取得最大值？
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

答案： 解:
(1)由题意,得OE=CD=80m,OC=ED=100m，AE=60m,BC=70m。
　
∴OA=OE−AE=20m,OB=OC−BC=30m。
　
∴点A(0,20),B(30,0)。
　　设直线AB的表达式为y=kx+b(k≠0),则$\begin{cases}b = 20\\30k + b = 0\end{cases}$，解得$\begin{cases}k = -\frac{2}{3}\\b = 20\end{cases}$。
　
∴直线AB的表达式为y= - $\frac{2}{3}$x+20。
(2)①设点P的坐标为P(x,y)。
　
∵点P在直线AB上，
　
∴点P的坐标可以表示为(x, - $\frac{2}{3}$x+20)。
　
∴PK=(100−x)m,
　　PH=80−( - $\frac{2}{3}$x+20)=(60 + $\frac{2}{3}$x)m
　
∴矩形PKDH的面积S与点P横坐标x之间的函数表达式为S=(100−x)(60 + $\frac{2}{3}$x)。
　　②
∵S=(100−x)(60 + $\frac{2}{3}$x)= - $\frac{2}{3}$(x−5)²+18050 / 3
　
∴当x=5时，S取得最大值。