《2025年考前示范卷九年级数学全一册人教版》

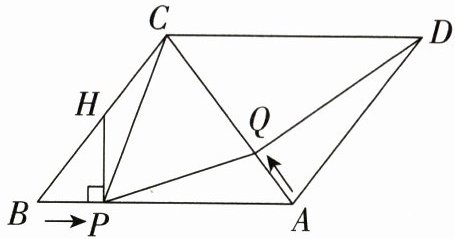
23. (12 分)如图，在▱ABCD 中，AC = BC = 10，AB = 12，动点 P 从点 B 出发，沿线段 BA 以每秒 2 个单位长度的速度向点 A 运动，过点 P 作 HP⊥BA 交 BC 于点 H;同时动点 Q 从点 A 出发，沿射线 AC 以每秒 2 个单位长度的速度向点 C 运动。设运动的时间为 t(0＜t＜5)秒。
(1)点 C 到边 AB 的距离为________;PH 的长度为________(用含 t 的代数式表示);
(2)是否存在某一时刻 t，使$S_{△PCQ}:S_{△DCO}=1:6$？若存在，求出 t 的值，若不存在，请说明理由;
(3)是否存在某一时刻 t，使点 P，Q，D 共线?若存在，求出 t 的值，若不存在，请说明理由。
　　

答案：
解:
(1)如图1，过点C作$CE⊥AB$于点E。
由题意，得$BP = 2t$。
∵$AC = BC$，
∴$BE = AE = \frac{1}{2}AB = 6$。
∴$CE = \sqrt{BC^2 - BE^2} = 8$。
∴点C到边AB的距离为8。
∵$HP⊥BA$，
∴$∠HPB = ∠CEB = 90°$。
∵$∠HBP = ∠CBE$，
∴$△HPB∽△CEB$。
∴$\frac{PH}{EC}=\frac{BP}{EB}$。
∴$\frac{PH}{8}=\frac{2t}{6}$。
∴$PH = \frac{8}{3}t$。
故答案为8，$\frac{8}{3}t$。

(2)存在$t$的值，使$S_{△PCQ}:S_{△ADC}=1:6$，理由如下：
如图2，过点P作$PG⊥AC$于点G，过点Q作$QF⊥CD$于点F。
由题意，得$∠AGP = ∠CFQ = 90°$，$BP = AQ = 2t$，$AP = 12 - 2t$，$CQ = 10 - 2t$。
∵四边形ABCD是平行四边形，
∴$AB// CD$，$AB = CD = 12$。
∴$∠PAG = ∠FCQ$。
∴$△APG∽△CQF$。
∴$\frac{PG}{QF}=\frac{AP}{CQ}=\frac{12 - 2t}{10 - 2t}$。
∴$\frac{S_{△PCQ}}{S_{△ADC}}=\frac{\frac{1}{2}CQ\cdot PG}{\frac{1}{2}CD\cdot QF}=\frac{CQ}{CD}\cdot\frac{PG}{QF}=\frac{10 - 2t}{12}\cdot\frac{12 - 2t}{10 - 2t}=\frac{1}{6}$。
解得$t = 5$。
当$t = 5$时，$10 - 2t = 0$，
∴$t = 5$为原分式方程的增根。
∴不存在$t$的值，使$S_{△PCQ}:S_{△ADC}=1:6$。
(3)存在某一时刻$t$，使点P，Q，D共线。如图3所示，

∵$AB// CD$，
∴$△APQ∽△CDQ$。
∴$\frac{AP}{CD}=\frac{AQ}{CQ}$。
∴$\frac{12 - 2t}{12}=\frac{2t}{10 - 2t}$。
化简，得$t^2 - 17t + 30 = 0$。
解得$t_1 = 15$，$t_2 = 2$。
∵$0 ＜ t ＜ 5$，
∴$t = 2$。
∴当$t = 2$时，点P，Q，D共线。

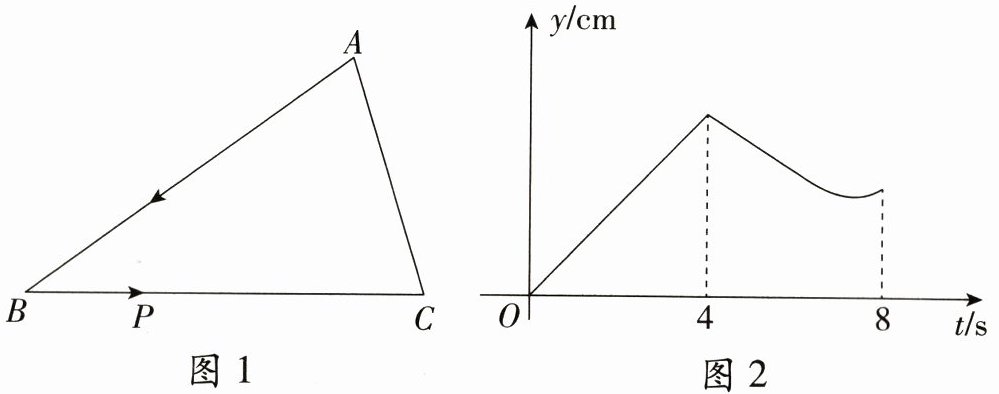
24. (10 分)如图 1，在△ABC 中，∠B = 36°，动点 P 从点 A 出发，沿折线 A→B→C 匀速运动至点 C 停止。若点 P 的运动速度为 1cm/s，设点 P 的运动时间为 t(s)，AP 的长度为 y(cm)，y 与 t 的函数图象如图 2 所示。
(1)当 AP 恰好平分∠BAC 时，求 t 的值;
(2)在(1)的条件下，求证:$BP² = BC\cdot PC$。
　　　　　　　　　　　　　　　　

答案：

(1)解:如图，当AP平分$∠BAC$时，连接AP。

由题图2，得$AB = BC = 4$cm。
∵$∠B = 36°$，$AB = BC$，
∴$∠BAC = ∠C = 72°$。
∵AP平分$∠BAC$，
∴$∠BAP = ∠PAC = ∠B = 36°$。
∴$AP = BP$，$∠APC = 72° = ∠C$。
∴$AP = AC = BP$。
∵$∠PAC = ∠B$，$∠C = ∠C$，
∴$△APC∽△BAC$。
∴$\frac{AP}{BA}=\frac{PC}{AC}$。
∴$AP\cdot AC = AB\cdot PC$。
∵$AP = AC$，
∴$AP^2 = AB\cdot PC = 4(4 - AP)$。
∴$AP = 2\sqrt{5} - 2 = BP$（负值已舍去）。
∴$t = (AB + BP)÷1 = (4 + 2\sqrt{5} - 2)÷1 = 2 + 2\sqrt{5}$。
(2)证明:由
(1)，知$AP^2 = AB\cdot PC$，
∵$AP = BP$，$AB = BC$，
∴$BP^2 = BC\cdot PC$。