《2025年考前示范卷九年级数学全一册人教版》

25.(10分)某水果超市以16元/千克购进一定数量的A种水果,若每千克售价为20元,每天可以售出120千克。经市场调查发现,在进价不变的情况下,每千克A种水果的售价每上涨2元,日销售量就减少10千克。
(1)若该水果超市希望每天销售A种水果盈利900元,则这个水果超市A种水果每千克的售价应上涨多少元？
(2)按照有关管理部门规定,该种水果的利润率不得高于75%,那么A种水果每千克的售价定为多少元,才能使每天所获利润最大？最大利润是多少?

答案： 解:
(1)设这个水果超市A种水果每千克的售价应上涨x元。
　　　　　　　根据题意,得(20+x−16)(120−10x$\frac{x}{2}$)=9000。
　　　　　　　解得x1=14,x2=6。
　
　
　
∴这个水果超市A种水果每千克的售价应上涨14元或6元。
(2)设每千克的售价定为y元，每天的利润为w元。
　　　　　　　w=(y−16)[120−$\frac{10}{2}$(y−20)]
　　　　　　　=−5y²+300y−3520
　　　　　　　=−5(y−30)²+980。
　
　
　
∵$\frac{y−16}{16}$×100%≤75%,
∴y≤28。
　
　
　
∵−5＜0,
∴当y＜30时,w随y的增大而增大。
　
　
　
∴当y=28时,w取最大值。
　
　
　
∴w=−5×4+980=960。
　
　
　
∴当该种水果每千克的售价定为28元，才能使每天所获利润最大，最大利润是960元。

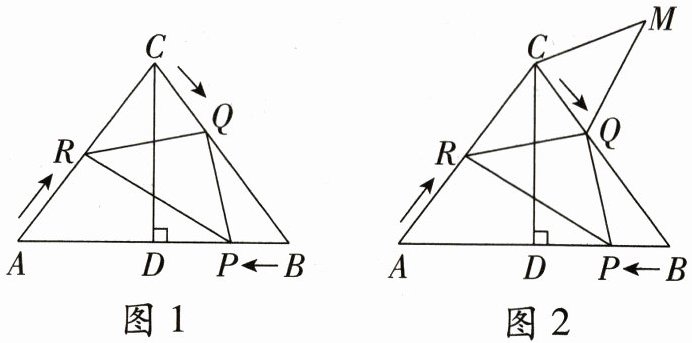
26.(10分)如图1,在△ABC中,AC=BC=10cm,CD⊥AB,CD=8cm,动点P以1cm/s的速度从点B 向点A运动;同时,动点Q从点C出发,以2cm/s的速度向点B运动,动点R从点A出发,以2cm/s的速度向点C运动,当其中一个点运动停止时,其他点的运动也停止,运动时间为t(s)
(0＜t＜5)。连接RQ,PR,PQ。
(1)当t为何值时,PR//BC?
(2)当S△BQP:S四边形CDPQ=1:4时,求t的值;
(3)如图2,沿CQ折叠△RCQ得到△MCQ,是否存在某一时刻t,使四边形RQMC为菱形？若存在,求出t的值;若不存在,请说明理由。

答案：
解:由题意,得AR=2tcm,BP=tcm,CQ=2tcm。
　
　
　
∵AC=BC=10cm,CD⊥AB,CD=8cm,
　
　
　
∴AD=BD=　$\sqrt{AC²−CD²}$=6cm。
　
　
　
∴AB=AD+BD=12cm。
　　　　　　　..CR=(10−2t)cm,BQ=(10−2t)cm,
AP=(12−t)cm。
　
　
　
∵PR//BC,
$\frac{AP}{AB}$。
　　　　　　　　120$\frac{12−t}{12}$。解得t=$\frac{60}{17}$。
　　　　10当为　为$\frac{60}{17}$时,PR//BC。
(2)由题意,得PB=tcm,AR=CQ=2tcm。
BQ=BC−CQ=(10−2t)cm。
　　　　如.当图S△B1O,过.点S边Q形e作DQ=E1⊥:4B时D,于S△点BOPE:。S△BC=1:5。

∵CD⊥AB,QE⊥AB,
∴QE//CD。
∴△QEB∽△CDB
∴$\frac{QE}{CD}$=$\frac{BQ}{BC}$。
∴$\frac{QE}{8}$$\frac{10−2t}{10}$。
∴QE=8$\frac{8}{5}$to
∴S△BP0=$\frac{1}{2}$×QE.BP=$\frac{1}{2}$x(8−$\frac{8}{5}$t).t.
∵S△BCD=$\frac{1}{2}$D.CD=$\frac{1}{2}$x6×8=24(cm²),
∴$\frac{1}{2}$x(8−58).t=$\frac{1}{5}$×24=$\frac{24}{5}$。
解得t=2或3。
∴当t=2或3时,S△BQP:S四边形cDPQ=1:4。
(3)沿CQ折叠△RCQ得到△MCQ,存在某一时刻t,使四边形RQMC为菱形。
如图2,过点R作RF⊥BC于点F,过点A作
AH⊥BC于点H。
　　　　　　
由题意,得PB=tcm,AR=CQ=2tcm。
∴RC=AC−AR=(10−2t)cm。
∵
∴△△MRCCQQ是△由M△CRQC。Q折叠形成的，　　若四边形RQMC为菱形，只需RC=RQ
∵RC=RQ,RF⊥BC,
　
　
　
　
∴CF=FQ=1CQ=tcm。
∵S△BAC=$\frac{1}{2}$xAB.CD=$\frac{1}{2}$xBC.AH,
　
∴12×8=10AH。
∴AH=9.6cm。
∵AH⊥BC,
∴∠AHC=90°。$\frac{一一}{AC=10}$
在Rt△AHC中,AH=9.6
∴CH=　$\sqrt{AC²−AH²}$=2.8cm。
∵RF⊥BC,AH⊥BC,
∴RF///AH。
∴△CRF∽△CAH
∴$\frac{CR}{CA}$=$\frac{CF}{CH}$。
∴$\frac{10−2t}{10}$=$\frac{t}{2.8}$。
解得t=$\frac{70}{39}$。
∴当t为$\frac{70}{39}$时，四边形RQMC为菱形。