《2025年考前示范卷九年级数学全一册人教版》

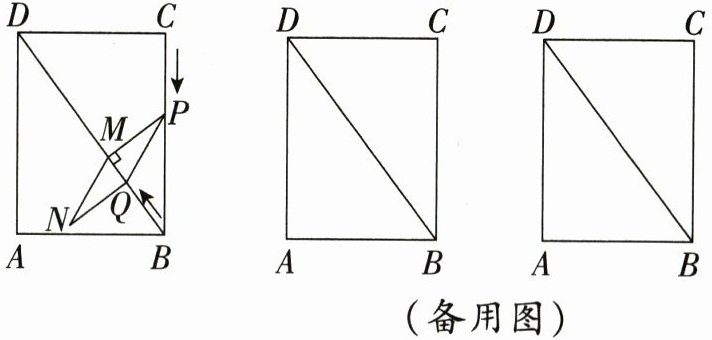
23. (9分)如图,在矩形ABCD中,AB = 6,BC = 8,点P从点C出发,沿CB向点B匀速运动,速度为每秒1个单位长度,过点P作PM⊥BD,交对角线BD于点M。点Q从点B出发,沿对角线BD向点D匀速运动,速度为每秒1个单位长度。P,Q两点同时出发,以PM,PQ为邻边作平行四边形PMNQ。设点P,Q的运动时间为t(0 ＜ t ＜ 8)秒。
(1) 当t = ________秒时,沿直线DP翻折,点C与点M重合;
(2) 当点N在AB上时,求t的值;
(3) 设平行四边形PMNQ的面积为S(cm²),求S与t之间的函数表达式,并求出相应的t的取值范围。

答案： 解:
(1)
∵四边形ABCD为矩形，AB = 6，BC = 8，
∴∠BCD = ∠BAD = 90°，AD = BC = 8，CD = AB = 6。
∴BD = $\sqrt{AB² + AD²}$ = $\sqrt{6² + 8²}$ = 10。
由题意，得CP = t，将△DCP沿直线DP翻折，点C与点M重合，
∴PM = t，∠DCP = ∠DMP = 90°，PB = 8 - t。
∵∠PMB = ∠DCB = 90°，∠PBM = ∠DBC，
∴△BMP∽△BCD。
∴$\frac{PM}{DC}$ = $\frac{PB}{DB}$，即$\frac{t}{6}$ = $\frac{8 - t}{10}$。
∴10t = 6(8 - t)。
∴10t = 48 - 6t。
∴16t = 48。
∴t = 3。
故答案为3。
(2)由
(1)知，△BMP∽△BCD。
∴$\frac{PM}{DC}$ = $\frac{BM}{BC}$ = $\frac{PB}{DB}$。
由题意，得PC = BQ = t。
∴PB = 8 - t。
∵AB = CD = 6，AD = BC = 8，BD = 10，
∴$\frac{PM}{6}$ = $\frac{BM}{8}$ = $\frac{8 - t}{10}$。
∴PM = $\frac{3}{5}$(8 - t)，BM = $\frac{4}{5}$(8 - t)。
∵四边形PMNQ为平行四边形，
∴NQ = PM = $\frac{3}{5}$(8 - t)，PM//NQ。
∵PM⊥BD，
∴AQ⊥BD。
当点N在AB上时，
∵∠NQB = ∠DAB = 90°，∠NBQ = ∠DBA，
∴△NQB∽△DAB。
∴$\frac{NQ}{DA}$ = $\frac{BQ}{BA}$，即$\frac{\frac{3}{5}(8 - t)}{8}$ = $\frac{t}{6}$。
∴$\frac{3}{5}$(8 - t)×6 = 8t。
∴$\frac{18}{5}$(8 - t) = 8t。
∴144 - 18t = 40t。
∴58t = 144。
∴t = $\frac{72}{29}$。
(3)由
(2)知，PM = $\frac{3}{5}$(8 - t)，BM = $\frac{4}{5}$(8 - t)。由题意，得PC = BQ = t。
∴MQ = BM - BQ = $\frac{4}{5}$(8 - t) - t = $\frac{32 - 4t - 5t}{5}$ = $\frac{32 - 9t}{5}$。
∵四边形PMNQ为平行四边形，
∴S四边形PMNQ = 2S△PMQ。
∴S = 2×$\frac{1}{2}$×PM×MQ = $\frac{3}{5}$(8 - t)×$\frac{32 - 9t}{5}$ = $\frac{3(8 - t)(32 - 9t)}{25}$ = $\frac{3(256 - 72t - 32t + 9t²)}{25}$ = $\frac{27}{25}t² - \frac{312}{25}t + \frac{768}{25}$。
∵S＞0，
∴$\frac{3}{5}$(8 - t)＞0，$\frac{32 - 9t}{5}$＞0。
∴t＜8且t＜$\frac{32}{9}$。
∴t＜$\frac{32}{9}$。
∵点P从点C出发，沿CB以每秒1个单位长度的速度运动，
∴0＜t＜8。
∴0＜t＜$\frac{32}{9}$。
∴S与t之间的函数表达式为S = $\frac{27}{25}t² - \frac{312}{25}t + \frac{768}{25}$，t的取值范围为0＜t＜$\frac{32}{9}$。