《2025年考前示范卷九年级数学全一册人教版》

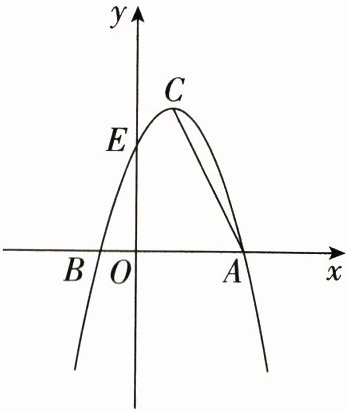
24.(10分)如图,抛物线y=−x²+2x+3交x轴于点A,B(点A在点B的右侧),交y轴于点E,其顶点为C,连接AC。
(1)求点A,B,E的坐标;
(2)求点C的坐标;
(3)若F为抛物线上一点,且∠CAF = 90°,求点F的坐标。
　　　　　　

答案： 解:
(1)
∵抛物线y = -x² + 2x + 3，令x = 0，得y = 3。
∴点E(0,3)。
令y = 0，得0 = -x² + 2x + 3，
解得x = 3或 -1。
∵点A在点B右侧，
∴xₐ＞x_b。
∴点A(3,0)，B(-1,0)。
(2)
∵抛物线y = -x² + 2x + 3 = -(x - 1)² + 4，
∴顶点C的坐标为(1,4)。
(3)如图，过点C作CH⊥x轴于点H，过点F作FG⊥x轴于点G。
设点F(m,-m² + 2m + 3)。
∵点A(3,0)，C(1,4)，
∴CH = 4，AH = 3 - 1 = 2，
FG = -m² + 2m + 3，AG = 3 - m。
∵CH⊥x轴，FG⊥x轴，∠CAF = 90°，
∴∠AHC = ∠FGA = 90°，∠CAH + ∠FAG = ∠CAH + ∠ACH = 90°。
∴∠ACH = ∠FAG。
∴△ACH∽△FAG。
∴$\frac{AH}{FG}$ = $\frac{CH}{AG}$。
∴$\frac{AG}{FG}$ = $\frac{CH}{AH}$ = $\frac{4}{2}$ = 2。
∴AG = 2FG。
∴3 - m = 2(-m² + 2m + 3)。
解得m = -$\frac{3}{2}$或3(不符合题意，舍去)。
此时 -m² + 2m + 3 = -(-$\frac{3}{2}$)² + 2×(-$\frac{3}{2}$) + 3 = $\frac{9}{4}$。
∴点F的坐标为(-$\frac{3}{2}$,$\frac{9}{4}$)。