2025年高中必刷题高二数学选择性必修第三册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年高中必刷题高二数学选择性必修第三册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
9. [河南部分学校2024高二期末联考]篮球运动员在比赛中每次罚球得分的规则是:命中得1分,不命中得0分. 已知某篮球运动员罚球命中的概率为0.8,设其罚球一次的得分为X,则 ( )
A. E(X)=0.5,D(X)=0.20
B. E(X)=0.5,D(X)=0.25
C. E(X)=0.8,D(X)=0.12
D. E(X)=0.8,D(X)=0.16
A. E(X)=0.5,D(X)=0.20
B. E(X)=0.5,D(X)=0.25
C. E(X)=0.8,D(X)=0.12
D. E(X)=0.8,D(X)=0.16
答案:
D 【解析】依题意,$X$ 的分布列为
| $X$ | 0 | 1 |
| ---- | ---- | ---- |
| $P$ | 0.2 | 0.8 |
因此 $E(X)=0.8$,$D(X)=E(X^2)-(E(X))^2=0.8 - 0.8^2 = 0.16$。故选 D。
| $X$ | 0 | 1 |
| ---- | ---- | ---- |
| $P$ | 0.2 | 0.8 |
因此 $E(X)=0.8$,$D(X)=E(X^2)-(E(X))^2=0.8 - 0.8^2 = 0.16$。故选 D。
10. [河南信阳2024高二月考]已知X,Y为随机变量,且E(X)=2,E(X²)=6,Y = 2X - 1,则D(Y)= ( )
A. 9
B. 8
C. 5
D. 4
A. 9
B. 8
C. 5
D. 4
答案:
B 【解析】由题意得,$D(X)=E(X^2)-(E(X))^2 = 6 - 4 = 2$,故 $D(Y)=D(2X - 1)=2^2D(X)=8$。故选 B。
规律方法 方差可由期望求出,记住公式 $D(X)=E(X^2)-(E(X))^2$,并学会根据方差与期望的定义进行推证。
规律方法 方差可由期望求出,记住公式 $D(X)=E(X^2)-(E(X))^2$,并学会根据方差与期望的定义进行推证。
11. [安徽安庆一中2023高二段考]若随机变量X的分布列为P(X = k)=pₖ,k = 1,2,3,且p₁ + 2p₂ + 3p₃ = 2,p₁ + 4p₂ + 9p₃ = $\frac{14}{3}$,则D(X)= ( )
A. 1
B. $\frac{4}{3}$
C. $\frac{2}{3}$
D. 4
A. 1
B. $\frac{4}{3}$
C. $\frac{2}{3}$
D. 4
答案:
C 【解析】根据题意可得 $E(X)=2$,$\sum_{i = 1}^{3}i^2p_i=\frac{14}{3}$,所以 $D(X)=\sum_{i = 1}^{3}i^2p_i-(E(X))^2=\frac{14}{3}-4=\frac{2}{3}$。故选 C。
12. [浙江宁波余姚中学2023高二月考]随机变量ξ的分布列如表所示,其中a,b,c成等差数列,则D(ξ) ( )
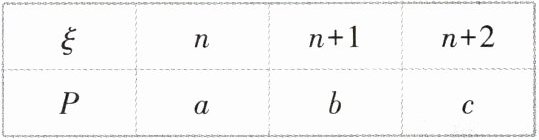
A. 与n有关,有最大值$\frac{2}{3}$
B. 与n有关,有最小值$\frac{2}{3}$
C. 与n无关,有最大值$\frac{2}{3}$
D. 与n无关,有最小值$\frac{2}{3}$
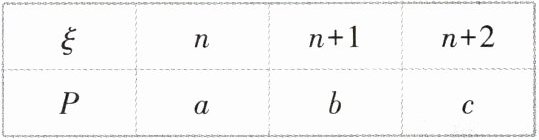
A. 与n有关,有最大值$\frac{2}{3}$
B. 与n有关,有最小值$\frac{2}{3}$
C. 与n无关,有最大值$\frac{2}{3}$
D. 与n无关,有最小值$\frac{2}{3}$
答案:
C 【解析】依题意,$a + c = 2b,a + b + c = 1$,所以 $b=\frac{1}{3}$,
$E(\xi)=na+(n + 1)b+(n + 2)c=n(a + b + c)+b + 2c=n + b + 2c$,
$E(\xi^2)=n^2a+(n + 1)^2b+(n + 2)^2c$,
所以 $D(\xi)=E(\xi^2)-(E(\xi))^2=n^2a+(n + 1)^2b+(n + 2)^2c-(n + b + 2c)^2=-4c^2+\frac{8}{3}c+\frac{2}{9}=-4(c-\frac{1}{3})^2+\frac{2}{3}(0\leq c\leq\frac{2}{3})$,
所以 $D(\xi)$ 与 $n$ 无关,且当 $c=\frac{1}{3}$ 时,$D(\xi)$ 有最大值 $\frac{2}{3}$。故选 C。
$E(\xi)=na+(n + 1)b+(n + 2)c=n(a + b + c)+b + 2c=n + b + 2c$,
$E(\xi^2)=n^2a+(n + 1)^2b+(n + 2)^2c$,
所以 $D(\xi)=E(\xi^2)-(E(\xi))^2=n^2a+(n + 1)^2b+(n + 2)^2c-(n + b + 2c)^2=-4c^2+\frac{8}{3}c+\frac{2}{9}=-4(c-\frac{1}{3})^2+\frac{2}{3}(0\leq c\leq\frac{2}{3})$,
所以 $D(\xi)$ 与 $n$ 无关,且当 $c=\frac{1}{3}$ 时,$D(\xi)$ 有最大值 $\frac{2}{3}$。故选 C。
13. [北京朝阳区2024高二期中]已知随机变量X的分布列如下:

若E(X)=1.2,则p = ________;当p = ________时,D(X)最大.

若E(X)=1.2,则p = ________;当p = ________时,D(X)最大.
答案:
0.1 0.2 【解析】由 $E(X)=1.2$,得 $0×p + 1×0.6+2×(0.4 - p)=1.2$,因此 $p = 0.1$。
依题意,$E(X)=1.4 - 2p,E(X^2)=0^2×p + 1^2×0.6+2^2×(0.4 - p)=2.2 - 4p$,
因此 $D(X)=E(X^2)-(E(X))^2=2.2 - 4p-(1.4 - 2p)^2=-4(p - 0.2)^2+0.4$,
则当 $p = 0.2$ 时,$D(X)$ 取得最大值。
依题意,$E(X)=1.4 - 2p,E(X^2)=0^2×p + 1^2×0.6+2^2×(0.4 - p)=2.2 - 4p$,
因此 $D(X)=E(X^2)-(E(X))^2=2.2 - 4p-(1.4 - 2p)^2=-4(p - 0.2)^2+0.4$,
则当 $p = 0.2$ 时,$D(X)$ 取得最大值。
14. 有甲、乙两种棉花,从中各抽取等量的样品进行检验,结果如下:

其中X表示纤维长度(单位:mm),根据纤维长度的均值和方差比较甲、乙两种棉花的质量.

其中X表示纤维长度(单位:mm),根据纤维长度的均值和方差比较甲、乙两种棉花的质量.
答案:
【解】由表中的数据,有 $E(X_{甲})=28×0.1+29×0.15+30×0.5+31×0.15+32×0.1 = 30$,
$E(X_{乙})=28×0.13+29×0.17+30×0.4+31×0.17+32×0.13 = 30$。
$D(X_{甲})=(28 - 30)^2×0.1+(29 - 30)^2×0.15+(30 - 30)^2×0.5+(31 - 30)^2×0.15+(32 - 30)^2×0.1 = 1.1$,
$D(X_{乙})=(28 - 30)^2×0.13+(29 - 30)^2×0.17+(30 - 30)^2×0.4+(31 - 30)^2×0.17+(32 - 30)^2×0.13 = 1.38$。
由上面的计算可知,尽管甲、乙两种棉花的纤维长度的均值相等,但 $D(X_{甲})=1.1<D(X_{乙})=1.38$,即甲品种棉花的纤维长度比乙品种棉花纤维长度更均匀一些,从这个意义上说,甲品种棉花的质量好于乙品种棉花的质量。
名师点拨 此类题一般优先选择均值较大的那个,如果均值相等,一般要用到方差,方差作为离散型随机变量的一个重要数字特征,刻画了随机变量取值的稳定与波动、集中与离散的程度,在均值相等的情况下,方差较小的比较稳定。
$E(X_{乙})=28×0.13+29×0.17+30×0.4+31×0.17+32×0.13 = 30$。
$D(X_{甲})=(28 - 30)^2×0.1+(29 - 30)^2×0.15+(30 - 30)^2×0.5+(31 - 30)^2×0.15+(32 - 30)^2×0.1 = 1.1$,
$D(X_{乙})=(28 - 30)^2×0.13+(29 - 30)^2×0.17+(30 - 30)^2×0.4+(31 - 30)^2×0.17+(32 - 30)^2×0.13 = 1.38$。
由上面的计算可知,尽管甲、乙两种棉花的纤维长度的均值相等,但 $D(X_{甲})=1.1<D(X_{乙})=1.38$,即甲品种棉花的纤维长度比乙品种棉花纤维长度更均匀一些,从这个意义上说,甲品种棉花的质量好于乙品种棉花的质量。
名师点拨 此类题一般优先选择均值较大的那个,如果均值相等,一般要用到方差,方差作为离散型随机变量的一个重要数字特征,刻画了随机变量取值的稳定与波动、集中与离散的程度,在均值相等的情况下,方差较小的比较稳定。
15. [江苏苏州2024高二期末]备战2024年法国巴黎奥运会(第33届夏季奥林匹克运动会)时,中国射击队女子50米汽步枪(三姿)队员苗婉茹、张琼月两名运动员展开队内对抗赛,比赛得分为两个相互独立的随机变量ξ与η,且ξ,η的分布列如下.

(1)求a,b的值;
(2)分别计算ξ,η的期望与方差,并以此分析苗婉茹、张琼月技术状况.

(1)求a,b的值;
(2)分别计算ξ,η的期望与方差,并以此分析苗婉茹、张琼月技术状况.
答案:
【解】
(1) 由离散型随机变量分布列的性质可知 $a + 0.1+0.6 = 1$,
$\therefore a = 0.3$。
同理 $0.3 + b+0.3 = 1$,解得 $b = 0.4$。
(2) $E(\xi)=1×0.3+2×0.1+3×0.6 = 2.3$,
$E(\eta)=1×0.3+2×0.4+3×0.3 = 2$,
$D(\xi)=(1 - 2.3)^2×0.3+(2 - 2.3)^2×0.1+(3 - 2.3)^2×0.6 = 0.81$,
$D(\eta)=(1 - 2)^2×0.3+(2 - 2)^2×0.4+(3 - 2)^2×0.3 = 0.6$。
答案及解析
由于 $E(\xi)>E(\eta)$,说明在一次射击中,苗婉茹的平均得分比张琼月高,但 $D(\xi)>D(\eta)$,说明苗婉茹得分的稳定性不如张琼月,因此苗婉茹、张琼月两人技术水平都不够全面,各有优势与劣势。
(1) 由离散型随机变量分布列的性质可知 $a + 0.1+0.6 = 1$,
$\therefore a = 0.3$。
同理 $0.3 + b+0.3 = 1$,解得 $b = 0.4$。
(2) $E(\xi)=1×0.3+2×0.1+3×0.6 = 2.3$,
$E(\eta)=1×0.3+2×0.4+3×0.3 = 2$,
$D(\xi)=(1 - 2.3)^2×0.3+(2 - 2.3)^2×0.1+(3 - 2.3)^2×0.6 = 0.81$,
$D(\eta)=(1 - 2)^2×0.3+(2 - 2)^2×0.4+(3 - 2)^2×0.3 = 0.6$。
答案及解析
由于 $E(\xi)>E(\eta)$,说明在一次射击中,苗婉茹的平均得分比张琼月高,但 $D(\xi)>D(\eta)$,说明苗婉茹得分的稳定性不如张琼月,因此苗婉茹、张琼月两人技术水平都不够全面,各有优势与劣势。
查看更多完整答案,请扫码查看


