2025年高中必刷题高二数学选择性必修第三册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年高中必刷题高二数学选择性必修第三册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. [北京第十二中学2023高二期中]某人射击一次命中目标的概率为$\frac{1}{2}$,每次射击的结果互不影响,则此人射击6次,3次命中且恰有2次连续命中的概率为 ( )
A. $\mathrm{C}_{6}^{3}(\frac{1}{2})^{6}$
B. $\mathrm{A}_{4}^{2}(\frac{1}{2})^{6}$
C. $\mathrm{C}_{4}^{2}(\frac{1}{2})^{6}$
D. $\mathrm{C}_{4}^{1}(\frac{1}{2})^{6}$
A. $\mathrm{C}_{6}^{3}(\frac{1}{2})^{6}$
B. $\mathrm{A}_{4}^{2}(\frac{1}{2})^{6}$
C. $\mathrm{C}_{4}^{2}(\frac{1}{2})^{6}$
D. $\mathrm{C}_{4}^{1}(\frac{1}{2})^{6}$
答案:
B【解析】根据每次射击命中目标的概率是$\frac{1}{2}$,且各次射击的结果互不影响,故此人射击6次,3次命中的概率为$C_{6}^{3}\cdot(\frac{1}{2})^{6}$,在有3次命中的前提下,恰有2次连续命中目标的概率为$\frac{A_{4}^{2}}{C_{6}^{3}}$,故此人射击6次,3次命中且恰有2次连续命中的概率为$C_{6}^{3}\cdot(\frac{1}{2})^{6}\cdot\frac{A_{4}^{2}}{C_{6}^{3}} = A_{4}^{2}(\frac{1}{2})^{6}$。故选B。
2. [河南南阳2024高二期末]2024年5月中国邮政发行了《巢湖》特种邮票3枚,巢湖是继《太湖》(5枚)、《鄱阳湖》(3枚)、《洞庭湖》(4枚)后,第四个登上特种邮票的五大淡水湖.现从15枚特种邮票中随机抽取2枚,记抽取邮票《巢湖》的枚数为X,则$E(X)=$ ( )
A. $\frac{2}{5}$
B. $\frac{2}{3}$
C. 1
D. $\frac{3}{2}$
A. $\frac{2}{5}$
B. $\frac{2}{3}$
C. 1
D. $\frac{3}{2}$
答案:
A【解析】依题意,$X$的所有可能取值有0,1,2,则$P(X = 0)=\frac{C_{12}^{2}}{C_{15}^{2}}=\frac{22}{35}$,$P(X = 1)=\frac{C_{12}^{1}C_{3}^{1}}{C_{15}^{2}}=\frac{12}{35}$,$P(X = 2)=\frac{C_{3}^{2}}{C_{15}^{2}}=\frac{1}{35}$,则$E(X)=0\times\frac{22}{35}+1\times\frac{12}{35}+2\times\frac{1}{35}=\frac{2}{5}$。故选A。
3. [山东临沂2024高二期末]随机变量$X\sim B(n,p)$,若$E(X)=1,D(X)=\frac{3}{4}$,则$P(X = 3)=$ ( )
A. $\frac{1}{16}$
B. $\frac{3}{64}$
C. $\frac{1}{64}$
D. $\frac{3}{256}$
A. $\frac{1}{16}$
B. $\frac{3}{64}$
C. $\frac{1}{64}$
D. $\frac{3}{256}$
答案:
B【解析】因为$X\sim B(n,p)$,所以$E(X)=np = 1$,$D(X)=np(1 - p)=\frac{3}{4}$,解得$p=\frac{1}{4}$,$n = 4$,所以$P(X = 3)=C_{4}^{3}(\frac{1}{4})^{3}(\frac{3}{4})^{1}=\frac{3}{64}$。故选B。
4. 已知在10件产品中可能存在次品,从中随机抽取2件进行检查,其次品数为X,已知$P(X = 1)=\frac{16}{45}$,且该产品的次品率不超过40%,则这10件产品的次品率为 ( )
A. 10%
B. 20%
C. 30%
D. 40%
A. 10%
B. 20%
C. 30%
D. 40%
答案:
B【解析】设10件产品中存在$n$件次品,从中随机抽取2件,其次品数为$X$,由$P(X = 1)=\frac{16}{45}$得$\frac{C_{n}^{1}\cdot C_{10 - n}^{1}}{C_{10}^{2}}=\frac{16}{45}$,化简得$n^{2}-10n + 16 = 0$,解得$n = 2$或$n = 8$。又$\because$该产品的次品率不超过40%,$\therefore n\leq4$,应取$n = 2$,即这10件产品的次品率为$\frac{2}{10}=20\%$。
5. [陕西西安长安区一中2023高二期末]甲、乙两队进行篮球决赛,采取七场四胜制(当一队赢得四场胜利时,该队获胜,决赛结束).根据前期比赛成绩,甲队的主客场安排依次为“主主客客主客主”.设甲队主场取胜的概率为0.6,客场取胜的概率为0.5,且各场比赛结果相互独立,则甲队以4:1获胜的概率是 ( )
A. $\frac{7}{20}$
B. $\frac{9}{50}$
C. $\frac{3}{20}$
D. $\frac{7}{50}$
A. $\frac{7}{20}$
B. $\frac{9}{50}$
C. $\frac{3}{20}$
D. $\frac{7}{50}$
答案:
【思路导引】比赛是七场四胜制,且有主客场切换。甲队以4:1获胜,则比赛进行了五场,且第五场甲队胜,前四场中甲队有一场输。因为前四场甲队的主客场安排为“主主客客”,甲队主场输和客场输的概率不同,故要分前四场中客场输和主场输两种情况讨论,分别计算概率再求和。
【解析】由题知,前四场中有一场客场输,第五场赢时,甲队以4:1获胜的概率是$0.6^{2}\times C_{2}^{1}0.5\times0.5\times0.6 = 0.108$;前四场中有一场主场输,第五场赢时,甲队以4:1获胜的概率是$C_{2}^{1}0.4\times0.6\times0.5^{2}\times0.6 = 0.072$。综上所述,甲队以4:1获胜的概率是$0.108 + 0.072 = 0.18=\frac{9}{50}$。故选B。
【解析】由题知,前四场中有一场客场输,第五场赢时,甲队以4:1获胜的概率是$0.6^{2}\times C_{2}^{1}0.5\times0.5\times0.6 = 0.108$;前四场中有一场主场输,第五场赢时,甲队以4:1获胜的概率是$C_{2}^{1}0.4\times0.6\times0.5^{2}\times0.6 = 0.072$。综上所述,甲队以4:1获胜的概率是$0.108 + 0.072 = 0.18=\frac{9}{50}$。故选B。
6. 我国古代认为构成宇宙万物的基本要素是金、木、土、水、火这五种物质,称为五行.五行的相生相克理论如图,即金生水,水生木,木生火,火生土,土生金;金克木,木克土,土克水,水克火,火克金. 依此理论,每次随机任取两行,重复取10次,若取出的两行为“生”的次数记为X,则$E(X)$与$D(X)$的值分别为 ( )
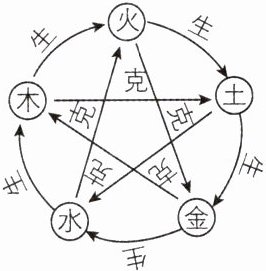
A. 1,$\frac{9}{10}$
B. 3,$\frac{21}{10}$
C. 5,$\frac{5}{2}$
D. 7,$\frac{21}{10}$

A. 1,$\frac{9}{10}$
B. 3,$\frac{21}{10}$
C. 5,$\frac{5}{2}$
D. 7,$\frac{21}{10}$
答案:
C【解析】设从五行中随机任取两行为“生”的事件为$A$,则$P(A)=\frac{5}{C_{5}^{2}}=\frac{1}{2}$。依题意,随机变量$X$服从二项分布,即$X\sim B(10,\frac{1}{2})$,故$E(X)=10\times\frac{1}{2}=5$,$D(X)=10\times\frac{1}{2}\times(1-\frac{1}{2})=\frac{5}{2}$,故选C。
7. [河北保定2024高二月考]高三(1)班有50名学生,其中30名男生,现从中任选3名学生参加体育抽测,用X表示男生被选中的人数,则$P(X\geq1)=$________;$E(X)=$________.
答案:
$\frac{923}{980}$,$\frac{9}{5}$【解析】因为事件$X\geq1$与事件$X = 0$互为对立事件,而$P(X = 0)=\frac{C_{20}^{3}}{C_{50}^{3}}=\frac{57}{980}$,所以$P(X\geq1)=1 - P(X = 0)=1-\frac{57}{980}=\frac{923}{980}$。
【敲黑板:互为对立事件的两个事件的概率之和为1】
所以$E(X)=n\frac{M}{N}=3\times\frac{30}{50}=\frac{9}{5}$。
【敲黑板:互为对立事件的两个事件的概率之和为1】
所以$E(X)=n\frac{M}{N}=3\times\frac{30}{50}=\frac{9}{5}$。
8. [辽宁大连八中2024高二月考]一个袋中装有10个大小相同的黑球、白球和红球. 已知从袋中任意摸出2个球,至少得到1个白球的概率是$\frac{7}{9}$.从袋中任意摸出3个球,记得到白球的个数为$\xi$,则随机变量$\xi$的数学期望$E(\xi)=$________.
答案:
$\frac{3}{2}$【解析】设白球的个数为$x(0\lt x\lt10,x\in N^{*})$,则黑球和红球的个数为$10 - x$,记摸出的两个球都不是白球的事件为$A$,则至少得到一个白球的事件与事件$A$为对立事件,所以$P(A)=1-\frac{7}{9}=\frac{2}{9}=\frac{C_{10 - x}^{2}}{C_{10}^{2}}$,解得$x = 5$,所以白球的个数为5。
从袋中任意摸出3个球,得到白球的个数$\xi$的取值可能为0,1,2,3,则$P(\xi = 0)=\frac{C_{5}^{0}C_{5}^{3}}{C_{10}^{3}}=\frac{1}{12}$,$P(\xi = 1)=\frac{C_{5}^{1}C_{5}^{2}}{C_{10}^{3}}=\frac{5}{12}$,$P(\xi = 2)=\frac{C_{5}^{2}C_{5}^{1}}{C_{10}^{3}}=\frac{5}{12}$,$P(\xi = 3)=\frac{C_{5}^{3}C_{5}^{0}}{C_{10}^{3}}=\frac{1}{12}$,所以$\xi$的分布列为:
|$\xi$|0|1|2|3|
| ---- | ---- | ---- | ---- | ---- |
|$P$|$\frac{1}{12}$|$\frac{5}{12}$|$\frac{5}{12}$|$\frac{1}{12}$|
所以$\xi$的数学期望$E(\xi)=0\times\frac{1}{12}+1\times\frac{5}{12}+2\times\frac{5}{12}+3\times\frac{1}{12}=\frac{3}{2}$。
从袋中任意摸出3个球,得到白球的个数$\xi$的取值可能为0,1,2,3,则$P(\xi = 0)=\frac{C_{5}^{0}C_{5}^{3}}{C_{10}^{3}}=\frac{1}{12}$,$P(\xi = 1)=\frac{C_{5}^{1}C_{5}^{2}}{C_{10}^{3}}=\frac{5}{12}$,$P(\xi = 2)=\frac{C_{5}^{2}C_{5}^{1}}{C_{10}^{3}}=\frac{5}{12}$,$P(\xi = 3)=\frac{C_{5}^{3}C_{5}^{0}}{C_{10}^{3}}=\frac{1}{12}$,所以$\xi$的分布列为:
|$\xi$|0|1|2|3|
| ---- | ---- | ---- | ---- | ---- |
|$P$|$\frac{1}{12}$|$\frac{5}{12}$|$\frac{5}{12}$|$\frac{1}{12}$|
所以$\xi$的数学期望$E(\xi)=0\times\frac{1}{12}+1\times\frac{5}{12}+2\times\frac{5}{12}+3\times\frac{1}{12}=\frac{3}{2}$。
9. 在一次新兵射击能力检测中,每人都可打5枪,只要击中靶标就停止射击,合格通过;5次全不中,则不合格. 新兵A参加射击能力检测,假设他每次射击相互独立,且击中靶标的概率均为$p(0 < p < 1)$,若当$p = p_{0}$时,他至少射击4次合格通过的概率最大,则$p_{0}=$________.
答案:
$1-\frac{\sqrt{15}}{5}$【解析】由题知,至少射击4次合格通过的概率为$f(p)=(1 - p)^{3}p+(1 - p)^{4}p=(1 - p)^{3}(2p - p^{2})$,所以$f'(p)=(1 - p)^{2}(5p^{2}-10p + 2)$。
【避坑:不要忘记$0\lt p\lt1$】
令$f'(p)=0$,解得$p = 1-\frac{\sqrt{15}}{5}$。
故$f(p)$在$(0,1-\frac{\sqrt{15}}{5})$上单调递增,在$(1-\frac{\sqrt{15}}{5},1)$上单调递减,所以当$p = 1-\frac{\sqrt{15}}{5}$时,$f(p)$取得最大值,故$p_{0}=1-\frac{\sqrt{15}}{5}$。
【名师点拨】用$f(p)$表示至少射击4次合格通过的概率,并利用导数研究其在$(0,1)$上的最值即可。
【避坑:不要忘记$0\lt p\lt1$】
令$f'(p)=0$,解得$p = 1-\frac{\sqrt{15}}{5}$。
故$f(p)$在$(0,1-\frac{\sqrt{15}}{5})$上单调递增,在$(1-\frac{\sqrt{15}}{5},1)$上单调递减,所以当$p = 1-\frac{\sqrt{15}}{5}$时,$f(p)$取得最大值,故$p_{0}=1-\frac{\sqrt{15}}{5}$。
【名师点拨】用$f(p)$表示至少射击4次合格通过的概率,并利用导数研究其在$(0,1)$上的最值即可。
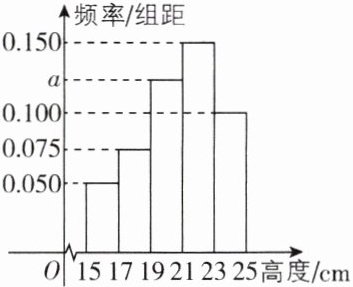
10. [四川成都树德中学2024高二期末]某植物园种植一种观赏花卉,这种观赏花卉的高度(单位:cm)介于[15,25]之间,现对植物园部分该种观赏花卉的高度进行测量,所得数据统计如图所示.
(1)求a的值;
(2)若从高度在[15,17)和[17,19)中采用分层随机抽样的方法抽取5株,在这5株中随机抽取3株,记高度在[15,17)内的株数为X,求X的分布列及数学期望$E(X)$;
(3)以频率估计概率,若在所有花卉中随机抽取3株,记高度在[15,17)内的株数为Y,求Y的数学期望.
(1)求a的值;
(2)若从高度在[15,17)和[17,19)中采用分层随机抽样的方法抽取5株,在这5株中随机抽取3株,记高度在[15,17)内的株数为X,求X的分布列及数学期望$E(X)$;
(3)以频率估计概率,若在所有花卉中随机抽取3株,记高度在[15,17)内的株数为Y,求Y的数学期望.

答案:
【解】
(1)由题意可知每组的频率依次为0.1,0.15,$2a$,0.3,0.2,因为$0.1 + 0.15+2a + 0.3+0.2 = 1$,解得$a = 0.125$。
(2)由
(1)可得高度在$[15,17)$和$[17,19)$内的频率分别为0.1和0.15,所以采用分层随机抽样的方法抽取的5株中,高度在$[15,17)$和$[17,19)$内的株数分别为2和3,则$X$的所有可能取值为0,1,2,则$P(X = 0)=\frac{C_{3}^{3}C_{2}^{0}}{C_{5}^{3}}=\frac{1}{10}$,$P(X = 1)=\frac{C_{3}^{2}C_{2}^{1}}{C_{5}^{3}}=\frac{3}{5}$,$P(X = 2)=\frac{C_{3}^{1}C_{2}^{2}}{C_{5}^{3}}=\frac{3}{10}$,所以$X$的分布列为:
|$X$|0|1|2|
| ---- | ---- | ---- | ---- | ---- |
|$P$|$\frac{1}{10}$|$\frac{3}{5}$|$\frac{3}{10}$|
数学期望为$E(X)=0\times\frac{1}{10}+1\times\frac{3}{5}+2\times\frac{3}{10}=\frac{6}{5}$。
(3)由
(1)知高度在$[15,17)$内的频率为0.1,所以用频率估计概率,可知高度在$[15,17)$内的概率为0.1,由题意可知$Y\sim B(3,0.1)$,所以$E(Y)=3\times0.1 = 0.3$。
(1)由题意可知每组的频率依次为0.1,0.15,$2a$,0.3,0.2,因为$0.1 + 0.15+2a + 0.3+0.2 = 1$,解得$a = 0.125$。
(2)由
(1)可得高度在$[15,17)$和$[17,19)$内的频率分别为0.1和0.15,所以采用分层随机抽样的方法抽取的5株中,高度在$[15,17)$和$[17,19)$内的株数分别为2和3,则$X$的所有可能取值为0,1,2,则$P(X = 0)=\frac{C_{3}^{3}C_{2}^{0}}{C_{5}^{3}}=\frac{1}{10}$,$P(X = 1)=\frac{C_{3}^{2}C_{2}^{1}}{C_{5}^{3}}=\frac{3}{5}$,$P(X = 2)=\frac{C_{3}^{1}C_{2}^{2}}{C_{5}^{3}}=\frac{3}{10}$,所以$X$的分布列为:
|$X$|0|1|2|
| ---- | ---- | ---- | ---- | ---- |
|$P$|$\frac{1}{10}$|$\frac{3}{5}$|$\frac{3}{10}$|
数学期望为$E(X)=0\times\frac{1}{10}+1\times\frac{3}{5}+2\times\frac{3}{10}=\frac{6}{5}$。
(3)由
(1)知高度在$[15,17)$内的频率为0.1,所以用频率估计概率,可知高度在$[15,17)$内的概率为0.1,由题意可知$Y\sim B(3,0.1)$,所以$E(Y)=3\times0.1 = 0.3$。
查看更多完整答案,请扫码查看


