2025年高中必刷题高二数学选择性必修第三册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年高中必刷题高二数学选择性必修第三册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 想要检验是否喜欢参加体育活动与性别有关联,应该检验 ( )
A. $H_{0}$:男性喜欢参加体育活动
B. $H_{0}$:女性不喜欢参加体育活动
C. $H_{0}$:喜欢参加体育活动与性别有关联
D. $H_{0}$:喜欢参加体育活动与性别无关联
A. $H_{0}$:男性喜欢参加体育活动
B. $H_{0}$:女性不喜欢参加体育活动
C. $H_{0}$:喜欢参加体育活动与性别有关联
D. $H_{0}$:喜欢参加体育活动与性别无关联
答案:
D 【解析】独立性检验假设有反证法的意味,应假设两分类变量(而非变量的属性)无关联,这时的$\chi^{2}$应该很小,若$\chi^{2}$很大,则可以否定假设,若$\chi^{2}$很小,则不能够肯定或者否定假设。
2. [辽宁省实验中学2023高二期中]现在,很多人都喜欢骑“共享单车”,但也有很多市民并不认可. 为了调查人们对这种交通方式的认可度,某同学从交通拥堵不严重的A城市和交通拥堵严重的B城市分别随机调查了20名市民,得到如下2×2列联表:
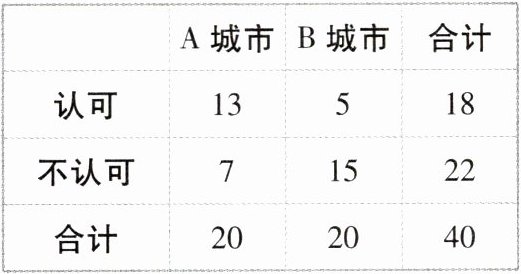
附:$\chi^{2}=\frac{n(ad - bc)^{2}}{(a + b)(c + d)(a + c)(b + d)}$,$n = a + b + c + d$.

根据表中的数据,下列说法中正确的是( )
A. 没有95%以上的把握认为“是否认可与城市的拥堵情况有关”
B. 有99%以上的把握认为“是否认可与城市的拥堵情况有关”
C. 可以在犯错误的概率不超过0.01的前提下认为“是否认可与城市的拥堵情况有关”
D. 可以在犯错误的概率不超过0.025的前提下认为“是否认可与城市的拥堵情况有关”

附:$\chi^{2}=\frac{n(ad - bc)^{2}}{(a + b)(c + d)(a + c)(b + d)}$,$n = a + b + c + d$.

根据表中的数据,下列说法中正确的是( )
A. 没有95%以上的把握认为“是否认可与城市的拥堵情况有关”
B. 有99%以上的把握认为“是否认可与城市的拥堵情况有关”
C. 可以在犯错误的概率不超过0.01的前提下认为“是否认可与城市的拥堵情况有关”
D. 可以在犯错误的概率不超过0.025的前提下认为“是否认可与城市的拥堵情况有关”
答案:
D 【解析】由题意,根据$2\times2$列联表中的数据,得$\chi^{2}=\frac{40\times(13\times15 - 5\times7)^{2}}{18\times22\times20\times20}\approx6.465$,又$5.024<6.465<6.635$,所以可以在犯错误的概率不超过$0.025$的前提下认为“是否认可与城市的拥堵情况有关”。故选D。
3. [浙江部分学校2024高二期中]为了评估一种新疫苗预防某疾病的效果,研究人员对一地区某种动物进行试验,从该试验群中随机进行了抽查. 已知抽查的接种疫苗的动物数量是没接种疫苗的2倍,接种且发病占接种的$\frac{1}{6}$,没接种且发病的占没接种的$\frac{1}{3}$,若本次抽查得出“在犯错误的概率不超过0.05的前提下认为接种该疫苗与预防某疾病有关”的结论,则被抽查的没接种的动物至少有 ( )
附:$\chi^{2}=\frac{n(ad - bc)^{2}}{(a + b)(c + d)(a + c)(b + d)}$,其中$n = a + b + c + d$.

A. 35只
B. 36只
C. 37只
D. 38只
附:$\chi^{2}=\frac{n(ad - bc)^{2}}{(a + b)(c + d)(a + c)(b + d)}$,其中$n = a + b + c + d$.

A. 35只
B. 36只
C. 37只
D. 38只
答案:
B 【解析】设没接种的动物数量为$k(k\in N^{*})$,依题意,得$2\times2$列联表如下:
| | 发病 | 没发病 | 合计 |
| --- | --- | --- | --- |
| 接种 | $\frac{k}{3}$ | $\frac{5k}{3}$ | $2k$ |
| 没接种 | $\frac{k}{3}$ | $\frac{2k}{3}$ | $k$ |
| 合计 | $\frac{2k}{3}$ | $\frac{7k}{3}$ | $3k$ |
则$\chi^{2}=\frac{3k(\frac{2k^{2}}{9}-\frac{5k^{2}}{9})^{2}}{\frac{2k}{3}\cdot\frac{7k}{3}\cdot2k\cdot k}=\frac{3k}{28}$,因为本次调查得出“在犯错误的概率不超过$0.05$的前提下认为接种该疫苗与预防某疾病有关”的结论,于是$\chi^{2}\geq3.841$,即$\chi^{2}=\frac{3k}{28}\geq3.841$,即$3k\geq3.841\times28$,所以$k > 35.85$,所以$k_{min}=36$。故选B。
| | 发病 | 没发病 | 合计 |
| --- | --- | --- | --- |
| 接种 | $\frac{k}{3}$ | $\frac{5k}{3}$ | $2k$ |
| 没接种 | $\frac{k}{3}$ | $\frac{2k}{3}$ | $k$ |
| 合计 | $\frac{2k}{3}$ | $\frac{7k}{3}$ | $3k$ |
则$\chi^{2}=\frac{3k(\frac{2k^{2}}{9}-\frac{5k^{2}}{9})^{2}}{\frac{2k}{3}\cdot\frac{7k}{3}\cdot2k\cdot k}=\frac{3k}{28}$,因为本次调查得出“在犯错误的概率不超过$0.05$的前提下认为接种该疫苗与预防某疾病有关”的结论,于是$\chi^{2}\geq3.841$,即$\chi^{2}=\frac{3k}{28}\geq3.841$,即$3k\geq3.841\times28$,所以$k > 35.85$,所以$k_{min}=36$。故选B。
4. (多选) [福建泉州五中2024一模]为了研究青少年玩手机时长与近视率的关系,现从某校随机抽查600名学生,经调查,其中有40%的学生近视,有20%的学生每天玩手机超过1小时,玩手机超过1小时的学生的近视率为50%. 用频率估计概率,则 ( )
附:$\chi^{2}=\frac{n(ad - bc)^{2}}{(a + b)(c + d)(a + c)(b + d)}$,其中$n = a + b + c + d$.

A. 若抽查的一名学生近视,则他每天玩手机超过1小时的概率为$\frac{1}{4}$
B. 若抽查的一名学生玩手机不超过1小时,则他近视的概率为$\frac{9}{25}$
C. 根据小概率值$\alpha = 0.05$的独立性检验,可以认为每天玩手机超过1小时会影响视力
D. 从该校抽查10位学生,每天玩手机超过1小时且近视的人数的期望为5
附:$\chi^{2}=\frac{n(ad - bc)^{2}}{(a + b)(c + d)(a + c)(b + d)}$,其中$n = a + b + c + d$.

A. 若抽查的一名学生近视,则他每天玩手机超过1小时的概率为$\frac{1}{4}$
B. 若抽查的一名学生玩手机不超过1小时,则他近视的概率为$\frac{9}{25}$
C. 根据小概率值$\alpha = 0.05$的独立性检验,可以认为每天玩手机超过1小时会影响视力
D. 从该校抽查10位学生,每天玩手机超过1小时且近视的人数的期望为5
答案:
AC 【解析】设$A =$“任选1名学生近视”,$B =$“任选1名学生每天玩手机超过1小时”,则$P(A)=\frac{2}{5}$,$P(B)=\frac{1}{5}$,$P(A|B)=\frac{1}{2}$,所以$P(AB)=P(B)P(A|B)=\frac{1}{10}$。
则$P(B|A)=\frac{P(AB)}{P(A)}=\frac{\frac{1}{10}}{\frac{2}{5}}=\frac{1}{4}$,故A正确;
因为$P(\overline{B}) = 1 - P(B)=\frac{4}{5}$,$P(A)=P(B)P(A|B)+P(\overline{B})P(A|\overline{B})=\frac{2}{5}$,即$\frac{1}{5}\times\frac{1}{2}+\frac{4}{5}P(A|\overline{B})=\frac{2}{5}$,解得$P(A|\overline{B})=\frac{3}{8}$,故B错误;
由题意,可得$2\times2$列联表如下:
| 视力 | 每天玩手机时长 | 合计 |
| --- | --- | --- |
| | 超过1小时 | 不超过1小时 |
| 近视 | 60 | 180 | 240 |
| 不近视 | 60 | 300 | 360 |
| 合计 | 120 | 480 | 600 |
由上表可知,$\chi^{2}=\frac{600\times(60\times300 - 180\times60)^{2}}{240\times360\times120\times480}=\frac{25}{4}=6.25>3.841$,所以根据小概率值$\alpha = 0.05$的独立性检验,可以认为每天玩手机超过1小时会影响视力,故C正确;
由题意知,从该校中任取1位学生,抽取到的学生每天玩手机超过1小时且近视的概率为$P(AB)=\frac{1}{10}$,设10位学生中每天玩手机超过1小时且近视的人数为$X$,则$X\sim B(10,\frac{1}{10})$,所以$E(X)=10\times\frac{1}{10}=1$,故D错误。故选AC。
则$P(B|A)=\frac{P(AB)}{P(A)}=\frac{\frac{1}{10}}{\frac{2}{5}}=\frac{1}{4}$,故A正确;
因为$P(\overline{B}) = 1 - P(B)=\frac{4}{5}$,$P(A)=P(B)P(A|B)+P(\overline{B})P(A|\overline{B})=\frac{2}{5}$,即$\frac{1}{5}\times\frac{1}{2}+\frac{4}{5}P(A|\overline{B})=\frac{2}{5}$,解得$P(A|\overline{B})=\frac{3}{8}$,故B错误;
由题意,可得$2\times2$列联表如下:
| 视力 | 每天玩手机时长 | 合计 |
| --- | --- | --- |
| | 超过1小时 | 不超过1小时 |
| 近视 | 60 | 180 | 240 |
| 不近视 | 60 | 300 | 360 |
| 合计 | 120 | 480 | 600 |
由上表可知,$\chi^{2}=\frac{600\times(60\times300 - 180\times60)^{2}}{240\times360\times120\times480}=\frac{25}{4}=6.25>3.841$,所以根据小概率值$\alpha = 0.05$的独立性检验,可以认为每天玩手机超过1小时会影响视力,故C正确;
由题意知,从该校中任取1位学生,抽取到的学生每天玩手机超过1小时且近视的概率为$P(AB)=\frac{1}{10}$,设10位学生中每天玩手机超过1小时且近视的人数为$X$,则$X\sim B(10,\frac{1}{10})$,所以$E(X)=10\times\frac{1}{10}=1$,故D错误。故选AC。
5. [江苏常州高级中学2024高二期末]某单位为了调查性别与对工作的满意程度是否具有相关性,随机抽取了若干名员工,所得数据统计如下表所示,其中$x\in N^{*}$,且$x < 6$. 若依据$\alpha = 0.05$的独立性检验,认为性别与对工作的满意程度具有相关性,则$x$的值是______.

附:$\chi^{2}=\frac{n(ad - bc)^{2}}{(a + b)(c + d)(a + c)(b + d)}$,其中$n = a + b + c + d$.


附:$\chi^{2}=\frac{n(ad - bc)^{2}}{(a + b)(c + d)(a + c)(b + d)}$,其中$n = a + b + c + d$.

答案:
5 【解析】根据独立性检验思想可得,$\chi^{2}=\frac{20x\cdot(36x^{2}-16x^{2})^{2}}{10x\cdot10x\cdot10x\cdot10x}=\frac{4x}{5}\geq3.841$,解得$x\geq4.80125$。因为$x\in N^{*}$且$x < 6$,所以$x = 5$。
查看更多完整答案,请扫码查看


