《2025年高中必刷题高二数学选择性必修第三册人教版》

1. [山东青岛即墨区第一中学2023高二期中]数轴上一个质点在随机外力的作用下，从原点0出发，每隔1秒向左或向右移动一个单位，已知向右移动的概率为$\frac{2}{3}$，向左移动的概率为$\frac{1}{3}$，共移动6次，则质点位于2的位置的概率是（ ）

A. $(\frac{2}{3})^{4}(\frac{1}{3})^{2}$
B. $(\frac{2}{3})^{2}(\frac{1}{3})^{4}$
C. $\mathrm{C}_{6}^{2}(\frac{2}{3})^{4}(\frac{1}{3})^{2}$
D. $\mathrm{C}_{6}^{2}(\frac{2}{3})^{2}(\frac{1}{3})^{4}$

答案： C【解析】此试验满足6重伯努利试验，每次向左移动的概率为$\frac{1}{3}$，向右移动的概率为$\frac{2}{3}$，设向左移动次数为$X$，根据从0移动到2，且移动6次，则需向右移动4次，向左移动2次，则$P(X = 2)=C_{6}^{2}(\frac{2}{3})^{4}(\frac{1}{3})^{2}$，故选C。

2. [黑龙江部分学校2024模拟]袋中装有标号为1,2,3,4,5且质地、大小相同的5个小球，从袋子中一次性摸出两个球，记下号码并放回，若两个号码的和是偶数，则获奖. 若有4人参与摸球，则恰好2人获奖的概率是（ ）
A. $\frac{216}{625}$
B. $\frac{324}{625}$
C. $\frac{8}{9}$
D. $\frac{27}{125}$

答案： A【解析】从袋子中一次性摸出两个球，共有$C_{5}^{2}=10$（种）情况，其中两个号码的和为偶数的有$\{1,3\}$，$\{1,5\}$，$\{2,4\}$，$\{3,5\}$，共4种情况，所以一个人摸球，能够获奖的概率为$\frac{4}{10}=\frac{2}{5}$，所以4人参与摸球，恰好2人获奖的概率$P = C_{4}^{2}\times(\frac{2}{5})^{2}\times(\frac{3}{5})^{2}=\frac{216}{625}$。故选A。

3. [陕西商洛2023高二月考]2023年苏迪曼杯世界羽毛球混合团体锦标赛半决赛中，中国队与日本队鏖战7小时，双方打满五局，最终中国队逆转战胜了日本队进入决赛. 这项比赛是五局三胜制，已知中国队每局获胜的概率为$\frac{2}{3}$，则中国队打满5局且最终获胜的概率为（ ）
A. $\frac{8}{243}$
B. $\frac{8}{81}$
C. $\frac{16}{81}$
D. $\frac{8}{27}$

答案： C
 思路导引
这类比赛题目要捋清比赛的规则和要求的获胜时对应的情况，此比赛为五局三胜制，要求中国队打满5局且最终获胜，则前4局中中国队恰好赢了2局、输了2局且第5局中国队获胜，再根据伯努利试验概率公式求解即可。
【解析】中国队打满5局且最终获胜，则前四局中中国队恰好赢了2局且第五局中国队获胜。因为每场比赛相互独立，所以中国队打满5局且最终获胜的概率为$C_{4}^{2}(\frac{2}{3})^{2}\times(\frac{1}{3})^{2}\times\frac{2}{3}=\frac{16}{81}$。故选C。

4. [河南信阳2024高二期末]随机变量$X\sim B(3,\frac{1}{2})$，则$P(X\geq1)=$（ ）
A. $\frac{7}{8}$
B. $\frac{2}{3}$
C. $\frac{1}{2}$
D. $\frac{1}{8}$

答案： A【解析】因为$X\sim B(3,\frac{1}{2})$，所以$P(X = k)=C_{3}^{k}(\frac{1}{2})^{3},k = 0,1,2,3$。所以$P(X\geq1)=1 - P(X = 0)=1 - C_{3}^{0}(\frac{1}{2})^{3}=\frac{7}{8}$。故选A。

5. [吉林白山2024高二期末]已知随机变量$X\sim B(n,0.5)$，当且仅当$k = 4$时，$P(X = k)$取得最大值，则$n=$（ ）
A. 7
B. 8
C. 9
D. 10

答案： B【解析】由题得$P(X = k)=C_{n}^{k}(\frac{1}{2})^{n},k = 0,1,\cdots,n$，由题知在$C_{n}^{0}(\frac{1}{2})^{n},C_{n}^{1}(\frac{1}{2})^{n},\cdots,C_{n}^{n}(\frac{1}{2})^{n}$中，最大值只有$C_{n}^{4}(\frac{1}{2})^{n}$，即在$C_{n}^{0},C_{n}^{1},\cdots,C_{n}^{n}$中，最大值只有$C_{n}^{4}$，所以由二项式系数的对称性可知$n = 8$。故选B。
＞敲黑板：当$n$是偶数时，中间的一项$C_{n}^{\frac{n}{2}}$取得最大值；当$n$是奇数时，中间的两项$C_{n}^{\frac{n - 1}{2}}$和$C_{n}^{\frac{n + 1}{2}}$相等，且同时取得最大值。

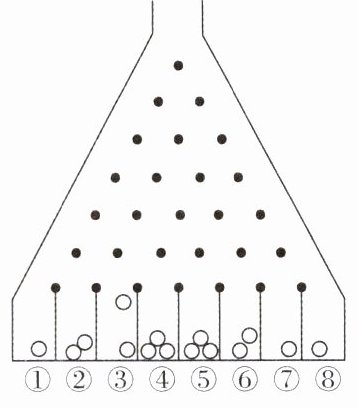
6. [辽宁东北育才学校2023高二月考]高尔顿钉板是英国生物学家高尔顿设计的，如图，每一个黑点表示钉在板上的一颗钉子，上一层的每个钉子水平位置恰好位于下一层的两颗钉子的正中间，从入口处放进一个直径略小于两颗钉子之间距离的白色圆玻璃球，白球向下降落的过程中，首先碰到最上面的钉子，碰到钉子后皆以二分之一的概率向左或向右滚下，于是又碰到下一层钉子. 如此继续下去，直到滚到底板的一个格子内为止. 现从入口放进一个白球，则其落在第③个格子的概率为（ ）


A. $\frac{1}{64}$
B. $\frac{15}{64}$
C. $\frac{21}{128}$
D. $\frac{35}{128}$

答案： C【解析】小球从起点到第③个格子一共跳了7次，其中向左边跳动5次，向右边跳动2次，小球每次向左或向右的概率均为$\frac{1}{2}$，则小球向右的次数服从二项分布$B(7,\frac{1}{2})$，所以所求概率为$P = C_{7}^{2}(\frac{1}{2})^{2}(\frac{1}{2})^{5}=\frac{21}{128}$，故选C。

7. [重庆巴蜀中学2024高二期末]某学校在假期组织30位学生前往北京、上海、广州、深圳、杭州、苏州、成都、重庆8个城市参加研学活动. 每个学生可自由选择8个城市中的任意1个（不要求每个城市必须要有学生选择）. 若每个学生选择去每个城市的概率都相等且互不影响，则选择前往北京或上海研学的概率最大的学生人数为（ ）
A. 6
B. 7
C. 8
D. 9

答案： B【解析】设有$X$个学生选择前往北京或上海研学，由题意可得每个学生选择前往北京或上海研学的概率$P=\frac{2}{8}=\frac{1}{4}$，则$X\sim B(30,\frac{1}{4})$，设有$k$个学生选择前往北京或上海研学的概率最大，则$\begin{cases}P(X = k)\geq P(X = k + 1)\\P(X = k)\geq P(X = k - 1)\end{cases}$，即$\begin{cases}C_{30}^{k}\cdot(\frac{1}{4})^{k}\cdot(\frac{3}{4})^{30 - k}\geq C_{30}^{k + 1}\cdot(\frac{1}{4})^{k + 1}\cdot(\frac{3}{4})^{29 - k}\\C_{30}^{k}\cdot(\frac{1}{4})^{k}\cdot(\frac{3}{4})^{30 - k}\geq C_{30}^{k - 1}\cdot(\frac{1}{4})^{k - 1}\cdot(\frac{3}{4})^{31 - k}\end{cases}$，即$\begin{cases}\frac{30!}{(30 - k)!\cdot k!}\cdot\frac{3}{4}\geq\frac{30!}{(29 - k)!\cdot(k + 1)!}\cdot\frac{1}{4}\\\frac{30!}{(30 - k)!\cdot k!}\cdot\frac{1}{4}\geq\frac{30!}{(31 - k)!\cdot(k - 1)!}\cdot\frac{3}{4}\end{cases}$，解得$\frac{27}{4}\leq k\leq\frac{31}{4}$。又$k\in N^{*}$，所以$k = 7$，所以有7个学生选择前往北京或上海研学的概率最大。故选B。

8. 在一次以“二项分布的性质”为主题的数学探究活动中，某中学高二某小组的学生表现优异，发现的正确结论得到老师和同学们的一致好评. 设随机变量$X\sim B(n,p)$，记$P_{k}=\mathrm{C}_{n}^{k}p^{k}\cdot(1 - p)^{n - k},k = 0,1,2,\cdots,n$. 在研究$P_{k}$的最大值时，该小组同学发现：若$(n + 1)p$为正整数，则当$k=(n + 1)p$时，$P_{k}=P_{k - 1}$，此时这两项概率均为最大值；若$(n + 1)p$为非整数，当$k$取$(n + 1)p$的整数部分时，$P_{k}$是唯一的最大值. 以此为理论基础，有同学重复投掷一枚质地均匀的骰子并实时记录点数1出现的次数，当投掷到第35次时，记录到此时点数1出现5次，若继续再进行65次投掷试验，即当投掷到第100次时，点数1一共出现的次数为_______的概率最大.

答案： 15或16【解析】继续再进行65次投掷试验，出现点数为1的次数$X$服从二项分布$B(65,\frac{1}{6})$。由$(n + 1)p = 66\times\frac{1}{6}=11$，结合题中的结论可知，当$k = 11$或$k = 10$时概率最大。即后面65次中出现11或10次点数1的概率最大，加上前面35次中出现点数1有5次，所以点数1出现15或16次的概率最大。