《2025年高中必刷题高二数学选择性必修第三册人教版》

1. [浙江宁波2023高二期中]一枚质地均匀的骰子,其六个面的点数分别为1,2,3,4,5,6. 现将此骰子任意抛掷2次,正面向上的点数分别为$X_1,X_2$. 设$Y_1=\begin{cases}X_1,X_1\geqslant X_2\\X_2,X_1＜X_2\end{cases}$,$Y_2=\begin{cases}X_1,X_1\leqslant X_2\\X_2,X_1＞X_2\end{cases}$,记事件$A=$“$Y_1 = 5$”,$B=$“$Y_2 = 3$”,则$P(B|A)=$ ( )
A. $\frac{1}{9}$
B. $\frac{2}{9}$
C. $\frac{1}{5}$
D. $\frac{2}{11}$

答案： B【解析】将此骰子任意抛掷2次，则样本空间中样本点的总数为36，显然$Y_1$是取大函数，所以$A = “Y_1 = 5”$，则$X_1$，$X_2$中有一个数字是5，另一个数字小于等于5，有$5×2 - 1 = 9$（种）情况。显然$Y_2$是取小函数，所以$A = “Y_1 = 5”$，$B = “Y_2 = 3”$同时发生，则有$(3,5)$和$(5,3)$两种情况，所以$P(A)=\frac{9}{36}=\frac{1}{4}$，$P(AB)=\frac{2}{36}=\frac{1}{18}$，所以$P(B|A)=\frac{P(AB)}{P(A)}=\frac{2}{9}$，故选B。

2. 如图所示的太极八卦图,八卦分据八方,中绘太极,古代常用此图作为除凶避灾的吉祥图案. 八卦中的每一卦均由纵向排列的三个爻组成,其中“”为阳爻,“”为阴爻. 现从八卦中任取两卦,已知取出的两卦中有一卦恰有一个阳爻,则另一卦至少有两个阳爻的概率为 ( )

A. $\frac{4}{7}$
B. $\frac{3}{7}$
C. $\frac{5}{6}$
D. $\frac{2}{3}$

答案： D【解析】由八卦图可知，八卦中有1卦有三个阳爻，有3卦恰有一个阳爻，有3卦恰有两个阳爻，有1卦没有阳爻。设取出的两卦中“有一卦恰有一个阳爻”为事件A，“另一卦至少有两个阳爻”为事件B。方法一：因为$P(A)=1 - P(\overline{A})=1-\frac{C_{5}^{2}}{C_{8}^{2}}=\frac{9}{14}$，$P(AB)=\frac{C_{3}^{1}C_{4}^{1}}{C_{8}^{2}}=\frac{3}{7}$，所以$P(B|A)=\frac{P(AB)}{P(A)}=\frac{2}{3}$。方法二：因为$n(A)=C_{3}^{1}C_{5}^{1}+C_{3}^{2}=18$，$n(AB)=C_{3}^{1}C_{4}^{1}=12$，所以$P(B|A)=\frac{n(AB)}{n(A)}=\frac{12}{18}=\frac{2}{3}$。

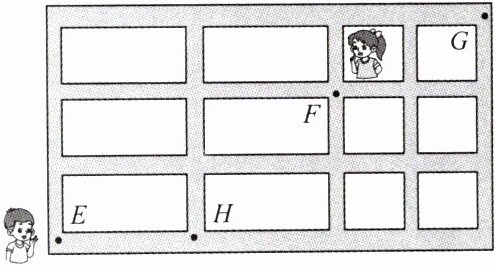
3. [四川成都石室中学2023入学考]小明与小红两位同学计划去养老院做义工. 如图,小明在街道E处,小红在街道F处,养老院位于G处,小明与小红到养老院都选择最短路径,两人约定在老年公寓门口会合,事件A:小明经过F;事件B:小明经过H;事件C:从F到养老院两人的路径没有重叠部分(路口除外),则下面说法正确的个数是 ( )
(1)$P(A)=\frac{18}{35}$;(2)$P(A|B)=\frac{9}{20}$;(3)$P(C|A)=\frac{2}{9}$.

A. 3
B. 2
C. 1
D. 0

答案： A【解析】小明到养老院能选择的最短路径条数为$C_{7}^{3}=35$；小明到F的最短路径有$C_{4}^{2}=6$条，再从F到养老院的最短路径有$C_{3}^{1}=3$条，故小明经过F到养老院能选择的最短路径条数为$6×3 = 18$，所以$P(A)=\frac{18}{35}$，故（1）正确；小明到H的最短路径有1条，从H到养老院的最短路径有$C_{6}^{3}=20$条，即$P(B)=\frac{20}{35}=\frac{4}{7}$，从H到F的最短路径有$C_{3}^{1}=3$条，从F到养老院的最短路径有3条，即$P(AB)=\frac{3×3}{35}=\frac{9}{35}$，所以$P(A|B)=\frac{P(AB)}{P(B)}=\frac{9}{20}$，故（2）正确；又$P(AC)=\frac{6×2}{35×3}=\frac{4}{35}$，所以$P(C|A)=\frac{P(AC)}{P(A)}=\frac{2}{9}$，故（3）正确。故选A。

4. (多选) [江苏盐城部分学校2024联考]如图,一个正八面体的八个面分别标有数字1到8,任意抛掷一次这个正八面体,观察它与地面接触的面上的数字X,得到样本空间$\Omega = \{1,2,3,4,5,6,7,8\}$,设事件$A = \{X\text{为奇数}\}$,事件$B = \{X＜5\}$,事件$C = \{3,4,6,8\}$,则 ( )

A. $P(ABC)=P(A)P(B)P(C)$
B. $P(B|C)=P(B|\overline{C})$
C. $P(A|B)=\frac{1}{2}$
D. $P(B\cup C)=1$

答案： ABC【解析】由题意可知，$A = \{1,3,5,7\}$，$B = \{1,2,3,4\}$，$C = \{3,4,6,8\}$，可得$P(A)=P(B)=P(C)=\frac{4}{8}=\frac{1}{2}$。\n对于选项A，因为$ABC = \{3\}$，所以$P(ABC)=\frac{1}{8}$，所以$P(ABC)=P(A)P(B)P(C)$，故A正确；\n对于选项B，因为$\overline{C}=\{1,2,5,7\}$，所以$B\overline{C}=\{1,2\}$，又$BC = \{3,4\}$，可得$P(B|C)=\frac{2}{4}=\frac{1}{2}$，$P(B|\overline{C})=\frac{2}{4}=\frac{1}{2}$，所以$P(B|C)=P(B|\overline{C})$，故B正确；\n对于选项C，因为$AB = \{1,3\}$，所以$P(A|B)=\frac{2}{4}=\frac{1}{2}$，故C正确；\n对于选项D，因为$B\cup C=\{1,2,3,4,6,8\}$，所以$P(B\cup C)=\frac{6}{8}=\frac{3}{4}$，故D错误。故选ABC。

5. (多选) [河北保定六校2024高二期中联考]对于一个电商平台,用户可以选择使用信用卡、支付宝或微信进行支付. 已知使用信用卡支付的用户占总用户的10%,使用支付宝支付的用户占总用户的45%,其余的用户使用微信支付. 平台试运营过程中发现三种支付方式都会遇到支付问题,为了优化服务进行数据统计,发现出现支付问题的概率是0. 067 5. 若一个遇到支付问题的用户,使用三种支付方式支付的概率均为$\frac{1}{3}$,则以下说法正确的是 ( )
A. 使用信用卡支付的用户中有20%的人遇到支付问题
B. 使用支付宝支付遇到支付问题与使用微信支付遇到支付问题的概率相同
C. 要将出现支付问题的概率降到0. 05,可以将信用卡支付通道关闭
D. 减少微信支付的人数有可能降低出现支付问题的概率

答案： BC【解析】根据题意，设用户使用信用卡支付为事件A，用户使用支付宝支付为事件B，用户使用微信支付为事件C，用户出现支付问题为事件E，则$P(A)=0.1$，$P(B)=0.45$，$P(C)=0.45$，$P(E)=0.0675$，且$P(A|E)=P(B|E)=P(C|E)=\frac{1}{3}$。\n对于A，由$P(A|E)=\frac{P(AE)}{P(E)}=\frac{P(A)P(E|A)}{P(E)}=\frac{0.1×P(E|A)}{0.0675}=\frac{1}{3}$，解得$P(E|A)=0.225$，故用户使用信用卡支付遇到支付问题的概率为22.5%，所以A错误；\n对于B，由$P(B|E)=\frac{P(BE)}{P(E)}=\frac{P(B)P(E|B)}{P(E)}=\frac{0.45×P(E|B)}{0.0675}=\frac{1}{3}$，解得$P(E|B)=0.05$，同理可得$P(E|C)=0.05$，所以$P(E|B)=P(E|C)$，即使用支付宝支付遇到支付问题与使用微信支付遇到支付问题的概率相同，所以B正确；\n对于C，如果将信用卡支付通道关闭，则$P(E)=P(B)P(E|B)+P(C)P(E|C)=P(B)P(E|B)+[1 - P(B)]P(E|C)$，又由B项可得$P(E|B)=P(E|C)=0.05$，则$P(E)=0.05$，即出现支付问题的概率降到0.05，故C正确；\n对于D，减少微信支付的人数，即$P(C)$减小，则$P(E)=P(A)P(E|A)+P(B)P(E|B)+P(C)P(E|C)=0.225P(A)+0.05P(B)+0.05P(C)$，若$P(C)$减小，则$P(E)$不变（由$P(A)+P(B)+P(C)=1$，若$P(C)$减小的加到$P(B)$中，$P(E)$不变；若$P(C)$减小的加到$P(A)$中，$P(E)$增大；若$P(C)$减小的加到$P(A)$和$P(B)$中，$P(E)$或增大），所以D错误。故选BC。

6. [河北石家庄二中2024高二期末]设A,B是一个随机试验中的两个事件,且$P(A)=\frac{2}{3}$,$P(B)=\frac{5}{12}$,$P(A\cup B)=\frac{5}{6}$,则$P(\overline{B}|\overline{A}) =$________.

答案： $\frac{1}{2}$【解析】因为$P(A)=\frac{2}{3}$，$P(B)=\frac{5}{12}$，所以$P(\overline{A})=1-\frac{2}{3}=\frac{1}{3}$，又$P(\overline{B}\cap\overline{A})=1 - P(A\cup B)=1-\frac{5}{6}=\frac{1}{6}$，则$P(\overline{B}|\overline{A})=\frac{P(\overline{B}\cap\overline{A})}{P(\overline{A})}=\frac{\frac{1}{6}}{\frac{1}{3}}=\frac{1}{2}$。