《2025年高中必刷题高二数学选择性必修第三册人教版》

1. [福建三明2023高二期中联考]下列说法正确的是 ( )
A. 若所有样本点都在经验回归直线$\hat{y}=\hat{b}x+\hat{a}$上,则变量间的样本相关系数为1
B. 经验回归方程为$\hat{y}=0.3 - 0.7x$时,变量$x$和$y$负相关
C. 在经验回归方程$\hat{y}=0.4 + 0.5x$中,当解释变量$x$每增加1个单位时,相应观测值$y$增加0.5个单位
D. 若变量$y$关于变量$x$的经验回归方程为$\hat{y}=\hat{b}x+\hat{a}$,则对所有的$x_{i}(i = 1,2,3,\cdots)$,预测值$\hat{b}x_{i}+\hat{a}$一定与实际观测值$y_{i}$有误差

答案： B 【解析】对于 A，样本相关系数 r = ±1，故 A 错误；
对于 B，因为斜率小于 0，所以变量 x 和 y 负相关，故 B 正确；
对于 C，在经验回归方程 $\hat{y}=0.4 + 0.5x$ 中，当解释变量 x 每增加 1 个单位时，相应观测值 y 约增加 0.5 个单位，并非一定增加 0.5 个单位，故 C 错误；
对于 D，可以存在 $x_i$，其对应的预测值 $\hat{b}x_i+\hat{a}$ 与实际值 $y_i$ 没有误差，故 D 错误。

2. [江苏南通2024高二期中]某产品的广告费用$x$(单位:万元)与销售额$y$(单位:万元)之间有如下关系：

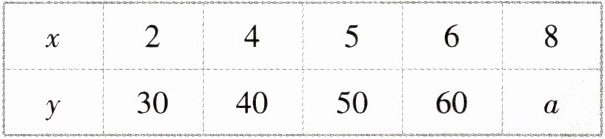
已知$y$与$x$的经验回归方程为$\hat{y}=7x + 15$,则$a$的值为 ( )

A. 68
B. 69
C. 70
D. 71

答案： C 【解析】由题意可知，$\bar{x}=\frac{1}{5}\times(2 + 4 + 5 + 6 + 8)=5$，
因为经验回归直线 $\hat{y}=7x + 15$ 过样本点的中心 $(\bar{x},\bar{y})$，所以 $\bar{y}=7\times5 + 15 = 50$。
故 $\frac{1}{5}\times(30 + 40 + 50 + 60 + a)=50$，解得 a = 70. 故选 C。

3. [河北邢台四校2024高二期末]已知某班学生的脚长$x$(单位:厘米)和身高$y$(单位:厘米)之间有线性相关关系,且其经验回归方程为$\hat{y}=4x + 70$. 若该班某学生的脚长为24厘米,则据此估计其身高为________.

答案： 166 厘米 【解析】由题意，令 x = 24，则 $\hat{y}=4\times24 + 70 = 166$，即估计该学生身高为 166 厘米。
→敲黑板：利用回归直线方程进行预测，实质是代入关系式中求值

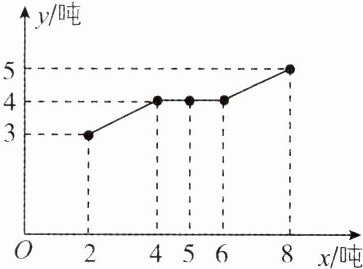
4. [四川绵阳实验高级中学2023高二检测]如图是某采矿厂的污水排放量$y$(单位:吨)与矿产品年产量$x$(单位:吨)的折线图.
(1)依据折线图计算样本相关系数$r$(精确到0.01),并据此判断是否可用线性回归模型拟合$y$与$x$的关系? (若$|r|＞0.75$,则线性相关程度很高,可用线性回归模型拟合)
(2)若可用线性回归模型拟合$y$与$x$的关系,请建立$y$关于$x$的经验回归方程,并预测年产量为10吨时的污水排放量.
参考数据:$\sqrt{0.3}\approx0.55,\sqrt{0.9}\approx0.95$.
相关公式:$r=\frac{\sum_{i = 1}^{n}(x_{i}-\overline{x})(y_{i}-\overline{y})}{\sqrt{\sum_{i = 1}^{n}(x_{i}-\overline{x})^{2}\sum_{i = 1}^{n}(y_{i}-\overline{y})^{2}}}$,经验回归方程$\hat{y}=\hat{b}x+\hat{a}$中,$\hat{b}=\frac{\sum_{i = 1}^{n}(x_{i}-\overline{x})(y_{i}-\overline{y})}{\sum_{i = 1}^{n}(x_{i}-\overline{x})^{2}},\hat{a}=\overline{y}-\hat{b}\overline{x}$.

答案： 【解】
(1)由题中折线图计算得
$\bar{x}=5,\bar{y}=4$，$\sum_{i = 1}^{5}(x_i-\bar{x})(y_i-\bar{y}) = 6$，
$\sum_{i = 1}^{5}(x_i-\bar{x})^2 = 20$，$\sum_{i = 1}^{5}(y_i-\bar{y})^2 = 2$，
所以样本相关系数 $r=\frac{6}{\sqrt{20}\times\sqrt{2}}$=$\sqrt{0.9}\approx0.95$， 因为 $|r|>0.75$，所以可用线性回归模型拟合 y 与 x 的关系。
(2)由
(1)及题中所给公式可得 $\hat{b}=\frac{6}{20}=0.3,\hat{a}=\bar{y}-\hat{b}\bar{x}=4 - 0.3\times5 = 2.5$， 所以经验回归方程为 $\hat{y}=0.3x + 2.5$， 当 x = 10 时，$\hat{y}=5.5$，所以年产量为 10 吨时的污水排放量预测为 5.5 吨。

5. 下列关于残差图的描述错误的是 ( )
A. 残差图的纵坐标只能是残差
B. 残差图的横坐标可以是编号、解释变量或响应变量
C. 残差点分布的带状区域的宽度越窄,残差平方和越小
D. 残差点分布的带状区域的宽度越窄,决定系数越小

答案： D 【解析】根据残差图的定义和图象即可得到结论. 可用残差图判断模型的拟合效果，残差点比较均匀地落在水平的带状区域中，说明这样的模型比较合适. 带状区域的宽度越窄，说明模型的拟合精度越高，则对应决定系数越大，故选项 D 错误. 故选 D。