《2025年高中必刷题高二数学选择性必修第三册人教版》

10. [四川雅安、广安部分学校2024高二期末联考]一名同学有4本不同的数学书,5本不同的物理书,3本不同的化学书,现要将这些书全部放在一个单层的书架上,且同科目的书不分开,则不同的放法种数为 ( )
A. $A_{3}^{3}A_{4}^{4}A_{5}^{5}$
B. $A_{4}^{4}A_{5}^{5}A_{6}^{6}$
C. $(A_{4}^{4})^{2}A_{5}^{5}A_{3}^{3}$
D. $A_{4}^{4}A_{5}^{5}(A_{3}^{3})^{2}$

答案： D 【解析】将同科目的书视为一个整体，排列 3 个科目的书有 $A_{3}^{3}$ 种方法，再分别排列同科目的书，分别有 $A_{4}^{4}$，$A_{5}^{5}$，$A_{3}^{3}$ 种方法，所以不同的放法种数为 $A_{4}^{4}A_{5}^{5}(A_{3}^{3})^{2}$. 故选 D.
高中必刷题 数学
特别注意
(1)相邻问题一般采用捆绑法，将相邻元素“捆绑”为一个元素，然后和其他元素进行排列.
(2)排列问题中注意关注同类元素是相同的还是不同的，本题中同科目的书是不同的，所以排列有顺序差异.

11. [湖南衡阳八中2024月考]在数学中,有一个被称为自然常数( 又叫欧拉数) 的常数e≈2.718 28. 小明在设置银行卡的数字密码时,打算将自然常数的前6位数字2,7,1,8,2,8进行某种排列得到密码. 如果排列时要求2不排第一个,两个8相邻,那么小明可以设置的不同的密码个数为 ( )
A. 30
B. 32
C. 36
D. 48

答案： C 【解析】由题意，设置的密码可分为 8 排第一位和 8 不排第一位两类：
若 8 排第一位，则两个 8 占第一、二位，再排 7 和 1 有 $A_{2}^{2}=12$（种），剩下的就是排 2，有 1 种，共有 $A_{2}^{2}=12$（种）.
方法一：若 8 不排第一位，则 7 或者 1 排第一位，有 2 种排法，两个 8 捆绑与两个 2，以及 7 和 1 剩的数排列，假设两个 2 有区别，则共有 $2A_{4}^{4}$ 种，但实际上两个 2 没有区别，故只有一半的数目，即共有 $\frac{2A_{4}^{4}}{2}=24$（种）.
方法二：若 8 不排第一位，则 7 或者 1 排第一位，共有 2 种；接着后面先放两个 2，然后在两个 2 的前中后 3 个位置中插入 7 或者 1 中剩余的一个数，共有 3 种；然后再插入捆绑的两个 8，共有 4 种，故共有 $2\times3\times4 = 24$（种）.
综上，设置的不同密码个数为 $12 + 24 = 36$，故选 C.

12. [安徽合肥八中等校2024高二期末联考]为积极落实“双减”政策,丰富学生的课外活动,某校开设了陶艺、剪纸、插花等5门课程,分别安排在周一到周五,每天一节,其中陶艺课不排在周一,剪纸和插花课相邻的课程安排方案种数为 ( )
A. 18
B. 24
C. 36
D. 42

答案： C 【解析】剪纸和插花课相邻的安排方法有 $A_{4}^{4}A_{2}^{2}=48$ 种，剪纸和插花课相邻且陶艺课排在周一的安排方法有 $A_{3}^{3}A_{2}^{2}=12$ 种，故陶艺课不排在周一，剪纸和插花课相邻的课程安排方案共有 $48 - 12 = 36$ 种，故选 C.

13. 某等候区有7个座位( 连成一排) ,甲、乙、丙三人随机就座,要求他们每两人之间至少有一个空位,则不同的坐法有 ( )
A. 4种
B. 10种
C. 20种
D. 60种

答案： D 【解析】甲、乙、丙每两人之间至少有一个空位，即甲、乙、丙互不相邻，相当于有四个空位放置成一排，形成 5 个空，甲、乙、丙三人插入这 5 个空中，所以有 $A_{5}^{3}=60$（种）不同的坐法，故选 D.

14. [湖南长沙2023高二期中]某校迎新晚会上有A,B,C,D,E,F共6个节目,为了考虑整体效果,对节目演出顺序有如下要求:节目A,B不相邻,节目D,F必须连在一起,则不同的节目编排方案种数为 ( )
A. 60
B. 72
C. 120
D. 144

答案： D 【解析】先将两个节目 D,F 捆绑成一个元素，与节目 C,E 进行全排列，再将节目 A,B 插入四个空中，则共有 $A_{2}^{2}A_{3}^{3}A_{4}^{2}=144$（种）不同的节目编排方案. 故选 D.

15. [河北石家庄二中2024高二月考]在古典名著《红楼梦》中有一道名为“茄鲞”的佳肴,这道菜用到了鸡汤、鸡脯肉、香菌、新笋、豆腐干、果干、茄子净肉七种原料,烹饪时要求香菌、新笋、豆腐干一起下锅,茄子净肉在鸡脯肉后下锅,最后加入精心熬制的鸡汤,则烹饪“茄鲞”时不同的下锅顺序共有 ( )
A. 72种
B. 36种
C. 12种
D. 6种

答案： C 【解析】将香菌、新笋、豆腐干看成一个元素，茄子净肉和鸡脯肉顺序一定，鸡汤最后下锅，所以不同的排序方法有 $\frac{A_{4}^{4}}{A_{2}^{2}}=12$ 种. 故选 C.
归纳总结 在有些排列问题中，某些元素的前后顺序是确定的（不一定相邻），解决这类问题的基本方法有两种：
(1)整体法，即若有 $(m + n)$ 个元素排成一列，其中 $m$ 个元素之间的先后顺序确定不变，先将这 $m + n$ 个元素排成一列，有 $A_{m + n}^{m + n}$ 种不同的排法，然后任取一个排列，固定其他 $n$ 个元素的位置不动，把这 $m$ 个元素交换顺序，有 $A_{m}^{m}$ 种排法，其中只有一个排列是我们需要的，因此共有 $\frac{A_{m + n}^{m + n}}{A_{m}^{m}}$ 种满足条件的不同排法.
(2)插空法，即 $m$ 个元素之间的先后顺序确定不变，因此先排这 $m$ 个元素，只有一种排法，然后把剩下的 $n$ 个元素分类或分步插入由以上 $m$ 个元素形成的空隙中.

16. 用3,4,5,6,7,9这六个数字组成没有重复数字的六位数,下列结论正确的是 ( )
A. 在这样的六位数中,奇数共有480个
B. 在这样的六位数中,3,5,7,9相邻的共有120个
C. 在这样的六位数中,4,6不相邻的共有504个
D. 在这样的六位数中,4个奇数从左到右按照从小到大排序的共有60个

答案： A 【解析】用 3,4,5,6,7,9 这 6 个数字组成没有重复数字的六位奇数，个位为 3,5,7,9 中的一个，有 4 种选法，其余五个数位上的数字进行全排列，有 $A_{5}^{5}$ 种，故这样的六位奇数共有 $4A_{5}^{5}=480$（个），A 正确；
在这样的六位数中，3,5,7,9 相邻，将 3,5,7,9 捆绑，有 $A_{4}^{4}$ 种排法，再与 4,6 进行全排列，有 $A_{3}^{3}$ 种排法，故共有 $A_{4}^{4}A_{3}^{3}=144$（个），B 错误；
在这样的六位数中，4,6 不相邻，先将 3,5,7,9 进行全排列，再从形成的五个空位中任选两个将 4,6 排列，故共有 $A_{4}^{4}A_{5}^{2}=480$（个），C 错误；
在这样的六位数中，4 个奇数从左到右按照从小到大排序的共有 $\frac{A_{6}^{6}}{A_{4}^{4}}=30$（个），D 错误.

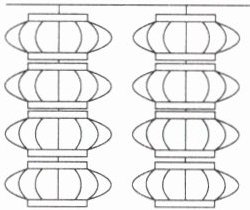
17. 元宵节灯展后,悬挂的8盏不同的花灯需要取下,如图所示,每次取1盏,则不同的取法共有 ( )

A. 32种
B. 70种
C. 90种
D. 280种

答案： B 【解析】因为取灯时每次只能取一盏，所以每串灯必须先取下面的灯，即每串灯取下的顺序确定，取下的方法有 $\frac{A_{8}^{8}}{A_{4}^{4}A_{4}^{4}}=70$（种）. 故选 B.

18. [重庆八中2024模拟]有6位同学排成一排准备拍照,拍照前加入了2位同学,如果要求他们仍站成一排,同时原来6位同学的相对顺序保持不变,则有________种不同的站法. ( 用数字作答)

答案： 56 【解析】因为共 8 位同学站成一排，原来 6 位同学的相对顺序保持不变，所以共有 $\frac{A_{8}^{8}}{A_{6}^{6}}=7\times8 = 56$（种）不同站法.

19. 现有8个人排成一排照相,其中甲、乙、丙三人不全相邻的排法种数为 ( )
A. $A_{6}^{6}\times A_{5}^{3}$
B. $A_{8}^{8}-A_{6}^{6}\times A_{3}^{3}$
C. $A_{5}^{3}\times A_{3}^{3}$
D. $A_{8}^{8}-A_{6}^{6}$

答案： B 【解析】在 8 个人全排列的方法数中减去甲、乙、丙全相邻的方法数，就得到甲、乙、丙三人不全相邻的方法数，即 $A_{8}^{8}-A_{6}^{6}\times A_{3}^{3}$. 故选 B.
易错警示 本题中“甲、乙、丙三人不全相邻”是指甲、乙、丙三人不能同时相邻，但允许其中有两人相邻，若将“甲、乙、丙三人不全相邻”误认为是“甲、乙、丙三人互不相邻”的情况，则会产生以下误解：甲、乙、丙三人以外的 5 人先排，有 $A_{5}^{5}$ 种排法，5 人排好后产生 6 个空，插入甲、乙、丙三人有 $A_{6}^{3}$ 种排法，这样共有 $A_{6}^{3}A_{5}^{5}$ 种排法，导致错选 A.

20. [广东清远多校2024高二期中联考]解不等式:$A_{8}^{x}＜6A_{8}^{x - 2}$.

答案： 【解】由 $A_{8}^{x}＜6A_{8}^{x - 2}$，得 $\frac{8!}{(8 - x)!}＜6\times\frac{8!}{(10 - x)!}$，$2\leq x\leq8$，
化简得 $x^{2}-19x + 84＜0$，解得 $7＜x＜12$，所以 $7＜x\leq8$.
由 $x\in N^{*}$，得 $x = 8$.
易错警示
(1)不要忽视公式 $A_{n}^{m}$ 中的条件“$m\leq n$”，如本题得到“$7＜x＜12$，且 $x\in N^{*}$，即 $x = 8,9,10,11$”的错误结论.
(2)不要忽视公式 $A_{n}^{m}$ 中的条件“$m,n\in N^{*}$”，如本题得到“$7＜x\leq8$”的错误结论.
(3)在解答排列数的方程或不等式时，要注意排列数 $A_{n}^{m}$，$m,n\in N^{*}$ 且 $m\leq n$ 这些限制条件，要注意含排列数的方程和不等式中未知数的取值范围.