2025年高中必刷题高二数学选择性必修第三册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年高中必刷题高二数学选择性必修第三册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 某学校的38个班级分别从6条不同的线路中选择一条进行研学游,则不同选法有 ( )
A. $\mathrm{A}_{38}^{6}$种
B. $\mathrm{C}_{38}^{6}$种
C. $6^{38}$种
D. $38^{6}$种
A. $\mathrm{A}_{38}^{6}$种
B. $\mathrm{C}_{38}^{6}$种
C. $6^{38}$种
D. $38^{6}$种
答案:
C【解析】38个班级,每个班级可选择的线路有6种,根据分步乘法计数原理得38个班级共有$6^{38}$种选法。故选C。
2. [福建泉州部分学校2024高二联考]某班联欢会原定5个节目,已排成节目单,开演前又增加了2个互动节目,现将这2个互动节目插入节目单中,要求互动节目既不排在第一位,也不排在最后一位,且不相邻,那么不同的插法种数为 ( )
A. 6
B. 10
C. 12
D. 20
A. 6
B. 10
C. 12
D. 20
答案:
C【解析】根据题意,原定5个节目之间有4个空位,从中选择2个安排互动节目即可,所以不同的插法种数为$A_{4}^{2}=12$。故选C。
3. [河北唐山2024高二期中]北斗七星是夜空中的七颗亮星,我国汉代纬书《春秋运斗枢》就有记载,它们组成的图形像我国古代舀酒的斗,故命名北斗七星. 北斗七星不仅是天上的星象,也是古人藉以判断季节的依据之一. 如图,用点A,B,C,D,E,F,G表示某季节的北斗七星,其中B,D,E,F看作共线,其他任何三点均不共线,若过这七个点中任意三个点作三角形,则所作的不同三角形的个数为 ( )
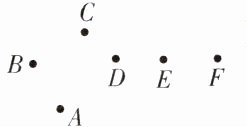
A. 35
B. 34
C. 31
D. 30
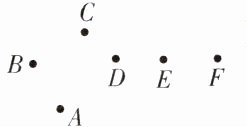
A. 35
B. 34
C. 31
D. 30
答案:
C【解析】从这七个点任意选取三个点有$C_{7}^{3}=35$种选法,从共线的四点中选取三点有$C_{4}^{3}=4$种选法,此时这三点不能构成三角形,故所作的不同三角形个数为$35 - 4 = 31$,故选C。
4. [广东深圳2023高二期中]在$(x^{2}-x+y)^{6}$的展开式中$x^{7}y$的系数为 ( )
A. 60
B. 30
C. 20
D. -60
A. 60
B. 30
C. 20
D. -60
答案:
D【解析】由$(x^{2}-x + y)^{6}=[(x^{2}-x)+y]^{6}$,可得其二项展开式通项为$T_{r + 1}=C_{6}^{r}(x^{2}-x)^{6 - r}y^{r}$,$r = 0,1,2,3,4,5,6$,若先满足$x^{7}y$中$y$的次数,则$r = 1$,可得$T_{2}=C_{6}^{1}(x^{2}-x)^{5}y = 6(x^{2}-x)^{5}y$,其中$(x^{2}-x)^{5}$展开式的通项为$T_{k + 1}'=C_{5}^{k}(x^{2})^{5 - k}(-x)^{k}=(-1)^{k}C_{5}^{k}x^{10 - k}$,$k = 0,1,2,3,4,5$,令$10 - k = 7$,得$k = 3$,可得$T_{4}'=(-1)^{3}C_{5}^{3}x^{7}=-10x^{7}$,故$x^{7}y$的系数为$6×(-10)= - 60$。故选D。
5. 若$(x+\frac{m}{x})(x - \frac{1}{x})^{5}$的展开式中常数项是10,则$m=$ ( )
A. -2
B. -1
C. 1
D. 2
A. -2
B. -1
C. 1
D. 2
答案:
D【解析】$(x+\frac{m}{x})(x-\frac{1}{x})^{5}=x(x-\frac{1}{x})^{5}+\frac{m}{x}(x-\frac{1}{x})^{5}$,$(x-\frac{1}{x})^{5}$的展开式的通项为$T_{r + 1}=C_{5}^{r}x^{5 - r}(-\frac{1}{x})^{r}=C_{5}^{r}(-1)^{r}x^{5 - 2r}(r = 0,1,2,\cdots,5)$。令$5 - 2r = - 1$,解得$r = 3$,则$x(x-\frac{1}{x})^{5}$的展开式的常数项为$-C_{5}^{3}=-10$。令$5 - 2r = 1$,解得$r = 2$,则$\frac{m}{x}(x-\frac{1}{x})^{5}$的展开式的常数项为$mC_{5}^{2}=10m$。因为$(x+\frac{m}{x})(x-\frac{1}{x})^{5}$的展开式中常数项是10,所以$10m - 10 = 10$,解得$m = 2$,故选D。
6. [重庆重点中学2024高二联考]中国是世界上最早发明雨伞的国家,伞是中国劳动人民一个重要的创造. 如图所示的雨伞,其伞面被伞骨分成8个区域,每个区域分别印有数字1,2,3,…,8. 现准备给该伞面的每个区域涂色,要求每个区域涂一种颜色,相邻两个区域所涂颜色不能相同,对称的两个区域(如区域1与区域5)所涂颜色相同. 若有6种不同颜色的颜料可供选择,则不同的涂色方案有 ( )

A. 550种
B. 630种
C. 720种
D. 840种

A. 550种
B. 630种
C. 720种
D. 840种
答案:
B【解析】由题意可得,只需确定区域1,2,3,4的颜色,即可确定整个伞面的颜色。先涂区域1,有6种选择,再涂区域2,有5种选择。当区域3与区域1的颜色不同时,区域3有4种选择,剩下的区域4有4种选择;当区域3与区域1的颜色相同时,剩下的区域4有5种选择。故不同的涂色方案有$6×5×(4×4 + 4×5)=630$种。故选B。
7. [山东菏泽2024高二期末]在$(2+\sqrt{x})^{2n + 1}(n\in\mathrm{N}^{*})$的展开式中,$x$的幂指数是整数的各项系数之和为 ( )
A. $3^{2n + 1}-1$
B. $3^{2n + 1}+1$
C. $\frac{3^{2n + 1}-1}{2}$
D. $\frac{3^{2n + 1}+1}{2}$
A. $3^{2n + 1}-1$
B. $3^{2n + 1}+1$
C. $\frac{3^{2n + 1}-1}{2}$
D. $\frac{3^{2n + 1}+1}{2}$
答案:
D【解析】设$A=(2+\sqrt{x})^{2n + 1}$,$B=(2-\sqrt{x})^{2n + 1}$,由二项式定理知$A$与$B$中的$x$的整数次幂项之和相同,记作$f(x)$,故有$2f(x)=(\sqrt{x}+2)^{2n + 1}+(-\sqrt{x}+2)^{2n + 1}$。令$x = 1$,则所求的系数之和为$f(1)=\frac{1}{2}(3^{2n + 1}+1)$。故选D。
8. [湖北武汉六中2023高二期中]现有天平和重量为1,2,4,10的砝码各一个,每一步,我们选取任意一个砝码,将其放入天平的左边或者右边,直至所有砝码全放到天平两边,但在放的过程中发现天平的指针不会偏向分度盘的右边,则这样的放法共有 ( )
A. 105种
B. 72种
C. 60种
D. 48种
A. 105种
B. 72种
C. 60种
D. 48种
答案:
A【解析】依题可知10只能在左边,按照从大到小的顺序,逐一分析情况:情况①:第一步先排10,10只能在左边,接下来重量为1,2,4的砝码顺序随意有$A_{3}^{3}$种,左右边随意,则有$2^{3}$种,共有$2^{3}A_{3}^{3}=48$(种)。\n情况②:第一步先排4,4只能在左边,10可以在第2,3,4步中任选一步放,有$C_{3}^{1}$种,重量为1,2的砝码顺序随意,左右边随意,共有$C_{3}^{1}2^{2}A_{2}^{2}=24$(种)。情况③:第一步先排2,2只能在左边,若第二步放10,则重量为1,4的砝码顺序随意,左右边随意,有$2^{2}A_{2}^{2}$种;若第二步放4,4只能放在左边,则10可以在第三、四步中任选一步放,砝码1左右边随意放,有$2C_{2}^{1}$种;若第二步放1,有2种放法,接下来第3步有2种情形:(a)若第三步放10,则第四步放4,砝码4左右边随意放,有2种;(b)若第三步放4,那4只能放左边,第四步放10只能放左边,有1种。
共有$2^{2}A_{2}^{2}+C_{2}^{1}×2 + 2×(2 + 1)=18$(种)。\n情况④:第一步先排1,1只能在左边,接下来第二步:若第二步放10,则重量为2,4的砝码顺序随意,左右边随意,有$2^{2}A_{2}^{2}$种;若第二步放4,4只能放在左边,则10可以在第三、四步中任选一步放,砝码2左右边随意放,有$2C_{2}^{1}$种;若第二步放2,2只能在左边,接下来第三步有2种情形:(a)若第三步放10,则第四步放4,砝码4左右边随意放,有2种;(b)若第三步放4,那4只能放左边,第四步放10只能放左边,有1种。
共有$2^{2}A_{2}^{2}+2C_{2}^{1}+2 + 1=15$(种)。
综上有$48 + 24 + 18 + 15=105$(种)放法。故选A。
共有$2^{2}A_{2}^{2}+C_{2}^{1}×2 + 2×(2 + 1)=18$(种)。\n情况④:第一步先排1,1只能在左边,接下来第二步:若第二步放10,则重量为2,4的砝码顺序随意,左右边随意,有$2^{2}A_{2}^{2}$种;若第二步放4,4只能放在左边,则10可以在第三、四步中任选一步放,砝码2左右边随意放,有$2C_{2}^{1}$种;若第二步放2,2只能在左边,接下来第三步有2种情形:(a)若第三步放10,则第四步放4,砝码4左右边随意放,有2种;(b)若第三步放4,那4只能放左边,第四步放10只能放左边,有1种。
共有$2^{2}A_{2}^{2}+2C_{2}^{1}+2 + 1=15$(种)。
综上有$48 + 24 + 18 + 15=105$(种)放法。故选A。
9. [安徽合肥一中2024高二期末]已知$m,n\in\mathrm{N}^{*}$且$n\geqslant m\gt1$,则下列等式恒成立的有( )
A. $\mathrm{A}_{n}^{m}=m\mathrm{A}_{n - 1}^{m - 1}$
B. $\mathrm{A}_{n + 1}^{n}-\mathrm{A}_{n}^{n}=n^{2}\mathrm{A}_{n - 1}^{n - 1}$
C. $\mathrm{C}_{3}^{3}+\mathrm{C}_{4}^{3}+\mathrm{C}_{5}^{3}+\cdots+\mathrm{C}_{2023}^{3}=\mathrm{C}_{2024}^{4}$
D. $(\mathrm{C}_{n}^{0})^{2}+(\mathrm{C}_{n}^{1})^{2}+\cdots+(\mathrm{C}_{n}^{n})^{2}=\mathrm{C}_{2n}^{n}$
A. $\mathrm{A}_{n}^{m}=m\mathrm{A}_{n - 1}^{m - 1}$
B. $\mathrm{A}_{n + 1}^{n}-\mathrm{A}_{n}^{n}=n^{2}\mathrm{A}_{n - 1}^{n - 1}$
C. $\mathrm{C}_{3}^{3}+\mathrm{C}_{4}^{3}+\mathrm{C}_{5}^{3}+\cdots+\mathrm{C}_{2023}^{3}=\mathrm{C}_{2024}^{4}$
D. $(\mathrm{C}_{n}^{0})^{2}+(\mathrm{C}_{n}^{1})^{2}+\cdots+(\mathrm{C}_{n}^{n})^{2}=\mathrm{C}_{2n}^{n}$
答案:
BD【解析】选项A,$A_{n}^{m}=\frac{n!}{(n - m)!}=n\cdot\frac{(n - 1)!}{[(n - 1)-(m - 1)]!}=nA_{n - 1}^{m - 1}$,故A错误;选项B,$A_{n + 1}^{n + 1}-A_{n}^{n}=(n + 1)!-n!=n!(n + 1 - 1)=n\cdot n!$,$n^{2}A_{n - 1}^{n - 1}=n^{2}(n - 1)!=n\cdot n!$,所以$A_{n + 1}^{n + 1}-A_{n}^{n}=n^{2}A_{n - 1}^{n - 1}$,故B正确;选项C,$C_{3}^{3}+C_{4}^{3}+C_{5}^{3}+\cdots +C_{2023}^{3}=C_{4}^{4}+C_{4}^{3}+C_{5}^{3}+\cdots +C_{2023}^{3}=C_{5}^{4}+C_{5}^{3}+\cdots +C_{2023}^{3}=\cdots =C_{2024}^{4}=C_{2024}^{2020}$,故C错误;选项D,二项式$(1 + x)^{2n}$展开式中$x^{n}$的系数是$C_{2n}^{n}$,又因为$(1 + x)^{2n}=(1 + x)^{n}\cdot(x + 1)^{n}$展开式中$x^{n}$的系数可写成$C_{n}^{0}\cdot C_{n}^{n}+C_{n}^{1}\cdot C_{n}^{n - 1}+\cdots +C_{n}^{n}\cdot C_{n}^{0}$,故D正确。
故选BD。
故选BD。
查看更多完整答案,请扫码查看


