《2025年高中必刷题高二数学选择性必修第三册人教版》

7. [山东聊城一中2023高二期中]某校从学生文艺部7名成员(4男3女)中,挑选2人参加学校举办的文艺汇演活动.
(1)求男生甲被选中的概率;
(2)在已知男生甲被选中的条件下,女生乙被选中的概率;
(3)在要求被选中的两人中必须是一男一女的条件下,求女生乙被选中的概率.

答案： 【解】（1）从7名成员中挑选2名成员，共有$C_{7}^{2}=21$（种）等可能的结果，记“男生甲被选中”为事件A，则事件A包含的结果有$C_{6}^{1}=6$（种），故$P(A)=\frac{6}{21}=\frac{2}{7}$。（2）记“女生乙被选中”为事件B。则$P(AB)=\frac{1}{21}$，又$P(A)=\frac{2}{7}$，故$P(B|A)=\frac{P(AB)}{P(A)}=\frac{\frac{1}{21}}{\frac{2}{7}}=\frac{1}{6}$。\n（3）记“被选中的两人是一男一女”为事件C，事件C所包含的结果有$C_{4}^{1}C_{3}^{1}=12$（种），则$P(C)=\frac{12}{21}=\frac{4}{7}$，$P(BC)=\frac{C_{4}^{1}}{21}=\frac{4}{21}$，故$P(B|C)=\frac{P(BC)}{P(C)}=\frac{\frac{4}{21}}{\frac{4}{7}}=\frac{1}{3}$。

8. [山西太原2024高二期末]在一个抽奖游戏中,主持人在编号分别为1,2,3的空箱(外观相同)中随机选择一个箱子放入奖品,并将箱子都关闭. 主持人知道奖品在哪个箱子里. 游戏规则:①抽奖人有两次选择箱子的机会,第一次在三个箱子中随机选择一个,在开箱之前,主持人只打开另外两个箱子中的一个空箱子(若此时两个箱子都是空的,则从中随机选取一个),并给抽奖人第二次选择箱子的机会,然后主持人按照抽奖人第二次的选择打开箱子;②若奖品在打开的箱子里,则奖品由抽奖人获得,否则,抽奖人未获得奖品;③游戏结束. 已知抽奖人第一次选择了1号箱.
(1)求主持人打开的空箱子是3号箱的概率.
(2)若主持人打开的空箱子是3号箱,则抽奖人是坚持选择1号箱,还是改选2号箱? 请你给出建议,并说明理由.

答案： 【解】（1）设$A_i = “奖品在第i号箱子里”(i = 1,2,3)$，$B = “主持人打开的空箱子是3号箱”$，由全概率公式，得$P(B)=P(A_1)\cdot P(B|A_1)+P(A_2)P(B|A_2)+P(A_3)\cdot P(B|A_3)=\frac{1}{3}×\frac{1}{2}+\frac{1}{3}×1+\frac{1}{3}×0=\frac{1}{2}$。（2）因为$P(A_1|B)=\frac{P(A_1B)}{P(B)}=\frac{P(A_1)P(B|A_1)}{P(B)}=\frac{1}{3}$，$P(A_2|B)=\frac{P(A_2B)}{P(B)}=\frac{P(A_2)P(B|A_2)}{P(B)}=\frac{2}{3}$，所以$P(A_1|B)＜P(A_2|B)$，则建议抽奖人改选2号箱。

9. [福建泉州2023高二月考]某足球队为评估球员的场上作用,对球员进行数据分析. 球员甲在场上担任边锋、前卫、中场三个位置,根据过往多场比赛,其出场率与出场时球队的胜率如下表所示.

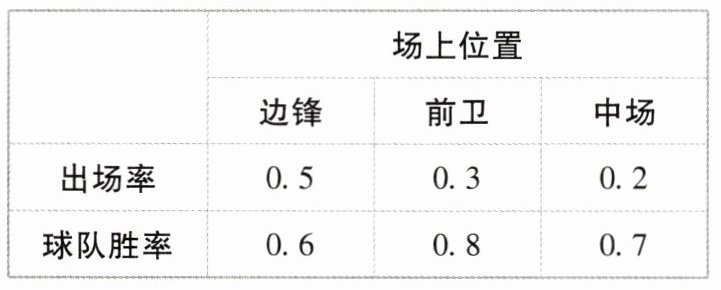
(1)当甲出场比赛时,求球队输球的概率.
(2)当甲出场比赛时,在球队获胜的条件下,求球员甲担任前卫的概率.
(3)如果你是教练员,将如何安排球员甲在场上的位置? 请说明安排理由.

答案： 【解】设$A_1$表示“甲球员担任边锋”，$A_2$表示“甲球员担任前卫”，$A_3$表示“甲球员担任中场”，B表示“球队赢了某场比赛”。\n（1）$P(B)=P(A_1)P(B|A_1)+P(A_2)P(B|A_2)+P(A_3)P(B|A_3)=0.5×0.6 + 0.3×0.8 + 0.2×0.7 = 0.30 + 0.24 + 0.14 = 0.68$，该球队某场比赛输球的概率为$1 - P(B)=1 - 0.68 = 0.32$。\n（2）由（1）知$P(B)=0.68$，所以$P(A_2|B)=\frac{P(A_2B)}{P(B)}=\frac{0.3×0.8}{0.68}=\frac{6}{17}$，所以在球队获胜的条件下，球员甲担任前卫的概率为$\frac{6}{17}$。\n（3）同（2）得$P(A_1|B)=\frac{P(A_1B)}{P(B)}=\frac{0.5×0.6}{0.68}=\frac{15}{34}$，$P(A_3|B)=\frac{P(A_3B)}{P(B)}=\frac{0.2×0.7}{0.68}=\frac{7}{34}$，由于$P(A_1|B)＞P(A_2|B)＞P(A_3|B)$，所以应多安排甲球员担任边锋，来增大赢球的概率。

10. [2024上海高三数学竞赛]现有甲、乙两人进行羽毛球比赛,已知每局比赛甲胜的概率为$\frac{1}{3}$,乙胜的概率为$\frac{2}{3}$,规定谁先胜3局谁赢得胜利,则甲赢得胜利的概率为________. (用最简分数表示答案)

答案： $\frac{17}{81}$【解析】比赛3局甲赢得胜利的概率$p_1 = (\frac{1}{3})^3=\frac{1}{27}$；比赛4局甲赢得胜利的概率$p_2 = C_{3}^{1}×(\frac{1}{3})^3×\frac{2}{3}=\frac{2}{27}$；比赛5局甲赢得胜利的概率$p_3 = C_{4}^{2}×(\frac{1}{3})^3×(\frac{2}{3})^2=\frac{8}{81}$。所以甲赢得胜利的概率为$p_1 + p_2 + p_3=\frac{3 + 6 + 8}{81}=\frac{17}{81}$。