《2026年新高考5年真题物理江苏专版》

8. [2024·广西卷,15T,16分] 某兴趣小组为研究非摩擦形式的阻力设计了如图甲的模型。模型由大齿轮、小齿轮、链条、阻力装置K及绝缘圆盘等组成。K由固定在绝缘圆盘上两个完全相同的环状扇形线圈$M_1$、$M_2$组成。小齿轮与绝缘圆盘固定于同一转轴上，转轴轴线位于磁场边界处，方向与磁场方向平行，匀强磁场磁感应强度大小为B，方向垂直纸面向里，与K所在平面垂直。大、小齿轮半径比为n，通过链条连接。K的结构参数见图乙，其中$r_1 = r$，$r_2 = 4r$，每个线圈的圆心角为$\pi - \beta$，圆心在转轴轴线上，电阻为R。不计摩擦，忽略磁场边界处的磁场。若大齿轮以ω的角速度保持匀速转动，以线圈$M_1$的ab边某次进入磁场时为计时起点，求K转动一周

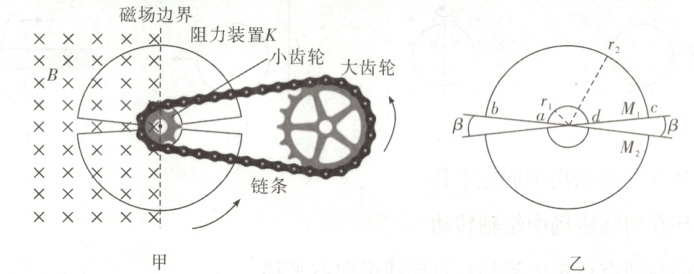
(1) 不同时间线圈$M_1$受到的安培力大小；
(2) 流过线圈$M_1$的电流有效值；
(3) 装置K消耗的平均电功率。

答案： 8.参考答案
(1)见解析
(2)$\frac{15nBr^{2}\omega}{2R}\sqrt{\frac{\pi - \beta}{\pi}}$
(3)$\frac{225(\pi - \beta)n^{2}B^{2}r^{4}\omega^{2}}{2\pi R}$
命题意图本题考查电磁感应、交变电流的有效值和电功率，考查考生的推理能力和分析综合能力。
解题思路
(1)由题意知大齿轮以$\omega$的角速度保持匀速转动，大、小齿轮的线速度相等，则$\omega_{1}=\frac{v}{r}$，$\omega=\frac{v}{nr}$，
可得小齿轮转动的角速度为$\omega_{1}=n\omega$，
转动周期为$T=\frac{2\pi}{\omega_{1}}=\frac{2\pi}{n\omega}$。
以线圈$M_{1}$的$ab$边某次进入磁场时为计时起点，到$cd$边进入磁场，经历的时间为$t_{1}=\frac{\pi - \beta}{2\pi}T=\frac{\pi - \beta}{n\omega}$，
这段时间内线圈$M_{1}$产生的电动势为$E_{1}=B×(4r - r)×\frac{v_{a}+v_{b}}{2}=B×3r×\frac{r\omega_{1}+4r\omega_{1}}{2}=\frac{15}{2}nBr^{2}\omega$，
电流为$I_{1}=\frac{E_{1}}{R}=\frac{15nBr^{2}\omega}{2R}$，
受到的安培力大小$F_{1}=BI_{1}L=B×\frac{15nBr^{2}\omega}{2R}×(4r - r)=\frac{45nB^{2}r^{3}\omega}{2R}$。
当$ab$边和$cd$边均进入磁场到$ab$边离开磁场，经历的时间为$t_{2}=\frac{\beta}{2\pi}T=\frac{\beta}{n\omega}$，
这段时间内穿过线圈$M_{1}$的磁通量不变，无感应电流，线圈$M_{1}$受到的安培力大小为0。
当线圈$M_{1}$的$ab$边离开磁场到$cd$边离开磁场，经历的时间为$t_{3}=t_{1}=\frac{\pi - \beta}{n\omega}$，
同理可知，这段时间内线圈$M_{1}$受到的安培力大小为$F_{3}=F_{1}=\frac{45nB^{2}r^{3}\omega}{2R}$，方向与进入时相反。
当线圈$M_{1}$的$cd$边离开磁场到$ab$边进入磁场，经历的时间为$t_{4}=t_{2}=\frac{\beta}{n\omega}$，
同理可知，这段时间内线圈$M_{1}$受到的安培力为0。
(2)设流过线圈$M_{1}$的电流有效值为$I$，则根据有效值定义有$I_{1}^{2}Rt_{1}+I_{2}^{2}Rt_{3}=I^{2}RT$，
其中$I_{1}=I_{3}$，$t_{1}=t_{3}$，
联立解得$I=\frac{15nBr^{2}\omega}{2R}\sqrt{\frac{\pi - \beta}{\pi}}$。
(3)根据题意可知流过线圈$M_{1}$和$M_{2}$的电流有效值相同，则在一个周期内装置$K$消耗的平均电功率为$P = 2I^{2}R=\frac{225(\pi - \beta)n^{2}B^{2}r^{4}\omega^{2}}{2\pi R}$。