《2025年期中期末名校名区真题精编高一物理上册人教版》

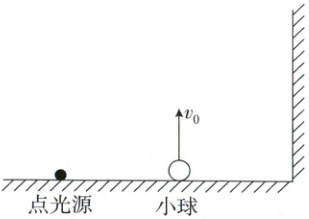
7. 如图所示，在水平面上固定一点光源，在点光源和右侧墙壁的正中间有一小球自水平面以初速度 $v_{0}$ 竖直上抛，已知重力加速度为 $g$，不计空气阻力，则在小球竖直向上运动的过程中，关于小球的影子在竖直墙壁上的运动情况，下列说法正确的是（ ）

A.影子做初速度为 $v_{0}$，加速度为 $g$ 的匀减速直线运动
B.影子做初速度为 $2v_{0}$，加速度为 $g$ 的匀减速直线运动
C.影子做初速度为 $2v_{0}$，加速度为 $2g$ 的匀减速直线运动
D.影子做初速度为 $v_{0}$，加速度为 $2g$ 的匀减速直线运动

答案： 7. C 本题主要考查运动的合成与分解 设小球上升的高度为$y$，影子在墙壁上的高度为$Y$，点光源、小球、影子的水平距离分别为$L$、$L$，由几何关系得$\frac{Y}{y} = \frac{2L}{L} = 2$，即$Y = 2y$。小球做竖直上抛运动，$y = v_0t - \frac{1}{2}gt^2$，则$Y = 2v_0t - gt^2$，可见影子做初速度为$2v_0$，加速度为$-2g$的匀减速直线运动，C 正确。

8. 伽利略对自由落体运动的研究实验，被评为十大最美物理实验之一。首先在斜面实验中发现物体运动的位移正比于所用时间的平方，改变斜面倾角时此规律仍然成立，于是伽利略认为自由落体运动也遵循同样的规律。下列说法正确的是（ ）

A.伽利略的做法是根据已有的论据凭直觉进行推论，缺乏严密的逻辑论证
B.伽利略在此过程中应用了合理外推这一科学推理方法
C.伽利略最终得出结论：自由落体运动是一种最简单的变速运动，其速度变化对于位移是均匀的
D.伽利略开创了以严密的数学演算为核心的近代科学

答案： 8. B 本题主要考查伽利略自由落体实验 伽利略的做法经历了提出问题、猜想与假设、数学推理、实验验证、合理外推、得出结论等科学步骤，不是凭直觉进行的推论，A 错误，B 正确；伽利略最终得出结论：自由落体运动是一种最简单的变速运动，其速度变化对于时间是均匀的，C 错误；伽利略开创了逻辑推理和实验验证相结合的近代科学，D 错误。

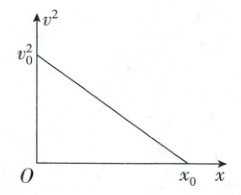
9. 如图所示是某物体做直线运动的 $v^{2} - x$ 图像（其中 $v$ 为速度，$x$ 为位置坐标），下列关于物体从 $x = 0$ 处运动至 $x = x_{0}$ 处的过程分析（$v_{0}$ 与 $x_{0}$ 为已知量），其中正确的是（ ）

A.该物体的加速度大小为 $\frac{v_{0}^{2}}{x_{0}}$
B.该物体运动前 $\frac{1}{2}x_{0}$ 与后 $\frac{1}{2}x_{0}$，所用时间之比为 $1:(\sqrt{2} + 1)$
C.当该物体的位移大小为 $\frac{1}{2}x_{0}$ 时，速度大小为 $\frac{1}{2}v_{0}$
D.当该物体的速度大小为 $\frac{1}{2}v_{0}$ 时，位移大小为 $\frac{3}{4}x_{0}$

答案： 9. BD 本题主要考查位移与速度关系式的推导与简单应用 由题图及匀变速直线运动的速度与位移关系式$v^2 - v_0^2 = -2ax$，可得$v^2 = -2ax + v_0^2$，$v^2 - x$图像斜率的绝对值等于$2a$，由图可得$2a = \frac{v_0^2}{x_0}$，则该物体的加速度大小为$a = \frac{v_0^2}{2x_0}$，A 错误；当该物体位移大小为$\frac{1}{2}x_0$时，由题图可得$v^2 = \frac{1}{2}v_0^2$，得$v = \frac{\sqrt{2}}{2}v_0$，由$\Delta v = at$，解得物体运动前$\frac{1}{2}x_0$与后$\frac{1}{2}x_0$，所用时间之比为$t_1 : t_2 = (v_0 - v) : (v - 0) = 1 : (\sqrt{2} + 1)$，B 正确，C 错误；当物体速度大小为$\frac{1}{2}v_0$时，$(\frac{1}{2}v_0)^2 = \frac{1}{4}v_0^2$，由题图可得$x = \frac{3x_0}{4}$，D 正确。