《2025年期中期末名校名区真题精编高一物理上册人教版》

11.（6 分）探究向心力大小 $ F $ 与小球质量 $ m $、角速度 $ \omega $ 和半径 $ r $ 之间关系的实验装置如图所示。匀速转动手柄，可使变速塔轮、长槽和短槽随之匀速转动，皮带分别套在两塔轮的圆盘上，可使两个槽内的小球分别以不同角速度做匀速圆周运动，小球做圆周运动的向心力由横臂上的挡板提供，同时小球对挡板的弹力使弹簧测力筒下降，露出测力筒内的标尺，标尺上露出的红白相间的等分格数之比即为两个小球所受向心力大小的比值。已知小球在挡板 $ A $、$ B $、$ C $ 处做圆周运动的轨迹半径之比为 $ 1:2:1 $。

（1）在这个实验中，利用了__________（选填“理想实验法”或“控制变量法”）来探究向心力的大小 $ F $ 与小球质量 $ m $、角速度 $ \omega $ 和半径 $ r $ 之间的关系。
（2）探究向心力的大小与圆周运动半径的关系时，应选择两个质量__________（选填“相同”或“不同”）的小球，分别放在挡板 $ C $ 与__________（选填“挡板 $ A $”或“挡板 $ B $”）处，同时用皮带分别套在半径相同的两个塔轮圆盘上。

答案： 11.
(1)控制变量法
(2)相同 挡板B
[解析] 本题主要考查探究向心力大小的表达式。
(1)本实验探究向心力的大小$F$与小球质量$m$、角速度$\omega$和半径$r$之间的关系，利用了控制变量法。
(2)本实验采用控制变量法，探究向心力的大小与圆周运动半径的关系时，需控制实验中小球质量、圆周运动角速度相同，只改变圆周运动半径，故应选择两个质量相同的小球，分别放在挡板C与挡板B处。

12.（8 分）用如图甲所示的实验装置探究“加速度与力、质量的关系”，实验时将一端带定滑轮的长木板放在水平实验桌上，小车通过细绳跨过定滑轮与砂桶相连，小车后端与纸带相连，打点计时器所用交流电的频率为 $ f = 50 Hz $。补偿阻力后，在保持小车质量不变的情况下放开砂桶，小车加速运动，处理纸带得到小车运动的加速度为 $ a $，改变砂桶中砂子的质量，重复实验五次。（计算结果均保留 2 位有效数字，重力加速度 $ g $ 取 $ 10 m/s^2 $）

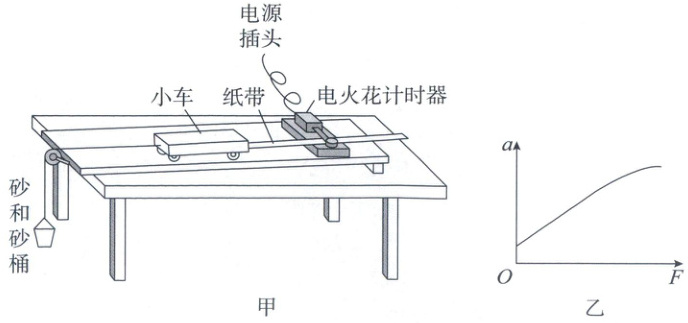
（1）在探究“质量一定，加速度 $ a $ 与合外力 $ F $ 的关系”时，某学生根据实验数据作出了如图乙所示的 $ a - F $ 图像，其中图线不过原点并在末端发生了弯曲，产生这两种现象的原因可能是__________。（填正确答案标号）
A. 木板右端垫起的高度过小
B. 木板右端垫起的高度过大
C. 砂桶和砂子的总质量 $ m $ 远小于小车的质量 $ M $
D. 砂桶和砂子的总质量 $ m $ 没有远小于小车的质量 $ M $
（2）实验过程中打出的一条理想纸带如图丙所示，图中 $ O $、$ A $、$ B $、$ C $、$ D $、$ E $、$ F $ 为相邻的计数点，相邻两计数点间还有 4 个计时点未画出，则打下 $ C $ 点时的速度 $ v_C = $__________ $ m/s $，小车运动的加速度 $ a = $__________ $ m/s^2 $。

（3）小车质量 $ M $ 一定，改变砂桶中砂子的质量，砂桶和砂子的总质量为 $ m $，根据实验数据描绘出的小车加速度 $ a $ 的倒数 $ \frac{1}{a} $ 与砂桶和砂子的总质量 $ m $ 的倒数 $ \frac{1}{m} $ 之间的 $ \frac{1}{a} - \frac{1}{m} $ 关系图像如图丁所示，则小车的质量 $ M = $__________ $ kg $。

答案： 12.
(1)BD
(2)0.70 2.0
(3)0.4
[解析] 本题主要考查探究加速度与力、质量的关系。
(1)$a - F$图线不过原点，即力为零时小车的加速度不为零，可能是由于木板右端垫起的高度过大(即平衡摩擦力过度)；$a - F$图线末端发生了弯曲现象，是砂桶和砂子的总质量$m$未满足远小于小车的质量$M$造成的，B、D正确。
(2)相邻两计数点间还有4个计时点未画出，则相邻两计数点间的时间间隔$T = 5 × \frac{1}{50}s = 0.1s$，纸带上C点的速度$v_{C} = \frac{x_{BD}}{2T} = 0.70m/s$，根据逐差法可得小车运动的加速度$a = \frac{x_{CF} - x_{OC}}{9T^{2}} = \frac{(7.98 + 10.01 + 11.99 - 2.00 - 3.96 - 6.02) × 10^{-2}}{9 × 0.1^{2}}m/s^{2} = 2.0m/s^{2}$。
(3)对小车、砂桶与砂子组成的系统，由牛顿第二定律可得$mg = (M + m)a$，整理得$\frac{1}{a} = \frac{M}{g} · \frac{1}{m} + \frac{1}{g}$。由题图丁可知$k = \frac{M}{g} = \frac{(0.5 - 0.1)s^{2} · m^{-1}}{10kg^{-1}}$，解得$M = 0.4kg$。