《2025年期中期末名校名区真题精编高一物理上册人教版》

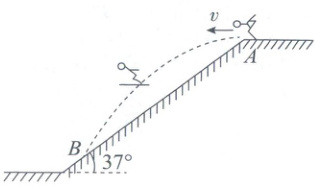
13.（12 分）跳台滑雪是勇敢者的运动，利用山势特点建造一个特殊跳台。一运动员脚踏专用滑雪板，不带雪杖，在助滑跑道上获得较大速度后从 $ A $ 点水平飞出，在空中飞行一段距离后在山坡上的 $ B $ 点着陆，如图所示。已知可视为质点的运动员水平飞出时的速度 $ v = 20 m/s $，山坡可看成倾角为 $ 37° $ 的斜面，不计空气阻力，重力加速度 $ g = 10 m/s^2 $，$ \sin 37° = 0.6 $，$ \cos 37° = 0.8 $。求：
（1）运动员在空中的飞行时间；
（2）运动员落到斜面上时的位移大小。

答案： 13.
(1)$3s$
(2)$75m$
[解析] 本题主要考查平抛运动。
(1)运动员水平飞出后做平抛运动，则$\tan 37^{\circ} = \frac{y}{x} = \frac{\frac{1}{2}gt^{2}}{vt} = \frac{gt}{2v}$解得$t = 3s$。
(2)运动员落到斜面上时的位移大小$x = \frac{vt}{\cos 37^{\circ}} = 75m$。
知识拓展：平抛运动与斜面相结合。斜面上的平抛运动问题是一种常见的题型，在解答这类问题时，除运用平抛运动的位移和速度规律外，还应充分运用斜面倾角，找出斜面倾角同位移和速度与水平方向间夹角的关系，从而使问题顺利解决。常见的模型如下：
方法 内容 斜面模型 总结
分解速度 水平速度：$v_{x} = v_{0}$ 分解速度，构建速度三角形
竖直速度：$v_{y} = gt$
合速度：$v = \sqrt{v_{x}^{2} + v_{y}^{2}}$
分解位移 水平位移：$x = v_{0}t$ 分解位移，构建位移三角形
竖直位移：$y = \frac{1}{2}gt^{2}$
合位移：$s = \sqrt{x^{2} + y^{2}}$