2025年期中期末名校名区真题精编高一物理上册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年期中期末名校名区真题精编高一物理上册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第27页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
7. 如图所示,水平地面上固定一表面粗糙的斜面体,斜面体顶端安装有定滑轮,轻绳1跨过定滑轮,一端连接物体A,另一端连接物体B;轻绳2绕过定滑轮,一端连接物体B,另一端人为控制。现让物体B缓慢由O点正下方P点沿虚线靠近Q点,O点和Q点等高,轻绳1一直处于张紧状态且物体A始终保持静止,不计空气阻力以及绳与滑轮间的摩擦力,滑轮大小可忽略,在物体B由P点运动到Q点的过程中,下列说法正确的是( )
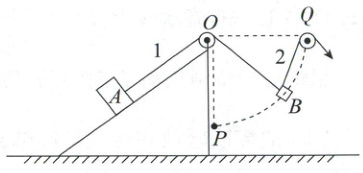
A.轻绳1的拉力大小先增大再减小
B.轻绳2的拉力一直变大
C.轻绳1和轻绳2对物体B的拉力的合力逐渐减小
D.物体A受到斜面的摩擦力一定是先减小后增大

A.轻绳1的拉力大小先增大再减小
B.轻绳2的拉力一直变大
C.轻绳1和轻绳2对物体B的拉力的合力逐渐减小
D.物体A受到斜面的摩擦力一定是先减小后增大
答案:
7.B 本题主要考查动态平衡 对物体B进行受力分析,如图所示
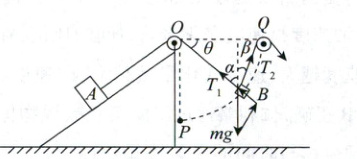
分析图中各夹角的几何关系,有$\alpha = 90^{\circ} - \theta$,$\beta = \frac{\theta}{2}$,根据正弦定理有$\frac{mg}{\sin(180^{\circ} - \alpha - \beta)} = \frac{T_1}{\sin\beta} = \frac{T_2}{\sin\alpha}$,即$\frac{mg}{\cos\frac{\theta}{2}} = \frac{T_1}{\sin\frac{\theta}{2}} = \frac{T_2}{\sin\alpha}$,所以$T_2 = \frac{\cos\theta}{\cos\frac{\theta}{2}}· mg=(2\cos\frac{\theta}{2}·\frac{\cos\theta}{\cos\frac{\theta}{2}})mg$,$T_1 = mg\tan\frac{\theta}{2}$,物体B由P点运动到Q点的过程中$\theta$减小,则$T_2$一直变大,$T_1$一直减小,A错误,B正确;由于物体B缓慢运动,即合外力为零,所以轻绳1和轻绳2对物体B的拉力的合力始终与物体B的重力等大反向,C错误;由于一开始物体A所受静摩擦力方向不确定,所以物体A受到斜面的摩擦力不一定是先减小后增大,D错误。
7.B 本题主要考查动态平衡 对物体B进行受力分析,如图所示

分析图中各夹角的几何关系,有$\alpha = 90^{\circ} - \theta$,$\beta = \frac{\theta}{2}$,根据正弦定理有$\frac{mg}{\sin(180^{\circ} - \alpha - \beta)} = \frac{T_1}{\sin\beta} = \frac{T_2}{\sin\alpha}$,即$\frac{mg}{\cos\frac{\theta}{2}} = \frac{T_1}{\sin\frac{\theta}{2}} = \frac{T_2}{\sin\alpha}$,所以$T_2 = \frac{\cos\theta}{\cos\frac{\theta}{2}}· mg=(2\cos\frac{\theta}{2}·\frac{\cos\theta}{\cos\frac{\theta}{2}})mg$,$T_1 = mg\tan\frac{\theta}{2}$,物体B由P点运动到Q点的过程中$\theta$减小,则$T_2$一直变大,$T_1$一直减小,A错误,B正确;由于物体B缓慢运动,即合外力为零,所以轻绳1和轻绳2对物体B的拉力的合力始终与物体B的重力等大反向,C错误;由于一开始物体A所受静摩擦力方向不确定,所以物体A受到斜面的摩擦力不一定是先减小后增大,D错误。
8. 如图所示,旅客在站台候车线处候车,相邻候车线间的距离以及每节车厢的长度均为L。列车进站时,从1号车厢的前端入口a点经过5号候车线时开始计时,到2号车厢的前端入口b点经过5号候车线时,所用的时间为T,列车停车时a点恰好正对1号候车线。若列车进站时做匀减速直线运动,则下列说法正确的是( )

A.列车进站时的加速度大小为$\frac{L}{T^{2}}$
B.a点经过2号候车线时,列车的瞬时速度大小为$2(7 - 4\sqrt{3})\frac{L}{T}$
C.从a点经过2号候车线到列车停止运动,经历的时间为$(2 + \sqrt{3})T$
D.从a点经过5号候车线到a点经过2号候车线的过程,列车的平均速度为$3(2 - \sqrt{3})\frac{L}{T}$

A.列车进站时的加速度大小为$\frac{L}{T^{2}}$
B.a点经过2号候车线时,列车的瞬时速度大小为$2(7 - 4\sqrt{3})\frac{L}{T}$
C.从a点经过2号候车线到列车停止运动,经历的时间为$(2 + \sqrt{3})T$
D.从a点经过5号候车线到a点经过2号候车线的过程,列车的平均速度为$3(2 - \sqrt{3})\frac{L}{T}$
答案:
8.CD 本题主要考查匀变速直线运动的推论 采用逆向思维可知,动车连续经过相等的位移所用的时间之比为$(\sqrt{4} - \sqrt{3}):(\sqrt{3} - \sqrt{2}):(\sqrt{2} - 1):1$,设列车从a点经过2号候车线到列车停止运动的时间为$t$,则有$\frac{t}{T} = \frac{1}{\sqrt{4} - \sqrt{3}}$,解得$t = (2 + \sqrt{3})T$,C正确;采用逆向思维,由公式$L = \frac{1}{2}at^2$,可得列车进站时的加速度大小为$a = \frac{2L}{t^2} = \frac{2L}{[(2 + \sqrt{3})T]^2}=2(7 - 4\sqrt{3})\frac{L}{T^2}$,A错误;a点经过2号候车线时,列车的瞬时速度大小$v_2 = at = 2(2 - \sqrt{3})\frac{L}{T}$,B错误;从a点经过5号候车线到a点经过2号候车线的过程,设列车经历的总时间$t'$,有$\frac{t'}{T} = \frac{1}{\sqrt{4} - \sqrt{3}} = 2 + \sqrt{3}$,解得$t' = (2 + \sqrt{3})T$,所以列车从a点经过5号候车线到a点经过2号候车线的过程中平均速度为$\bar{v} = \frac{3L}{t'}=3(2 - \sqrt{3})\frac{L}{T}$,D正确。
9. 曲柄连杆结构是发动机实现工作循环和完成能量转化的主要部件。如图所示,连杆下端连接活塞Q,上端连接曲轴P。在工作过程中,活塞Q在汽缸内上下做直线运动,带动曲轴绕圆心O旋转,若P做线速度大小为$v_{0} = 12m/s$的匀速圆周运动,已知$OP:PQ = 3:4$,则下列说法正确的是( )
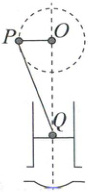
A.当OP与OQ垂直时,活塞运动的速度等于12m/s
B.当O、P、Q在同一直线时,活塞运动的速度为零
C.当PQ垂直于OP时,活塞运动的速度为10m/s
D.当PQ垂直于OP时,活塞运动的速度为15m/s

A.当OP与OQ垂直时,活塞运动的速度等于12m/s
B.当O、P、Q在同一直线时,活塞运动的速度为零
C.当PQ垂直于OP时,活塞运动的速度为10m/s
D.当PQ垂直于OP时,活塞运动的速度为15m/s
答案:
9.ABD 本题主要考查关联速度 对P和Q的运动分解,如图所示
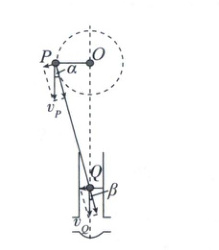
由关联速度可知$v_P\cos\alpha = v_Q\cos\beta$,则$v_Q = \frac{\cos\alpha}{\cos\beta}v_P$,当OP与OQ垂直时,$\alpha = \beta$,曲轴P速度的大小为$v_0$,可知活塞运动的速度等于P点的速度,都是$v_0 = 12m/s$,A正确;当O、P、Q在同一直线时,P点的速度方向与OQ方向垂直,沿OQ方向的分速度为零,Q的瞬时速度为零,所以活塞运动的速度等于零,B正确;当PQ垂直于OP时,即杆与圆相切,$v_Q = \frac{v_0}{\cos\beta}$,根据几何关系可得$\cos\beta = \frac{4}{5}$,解得$v_Q = 15m/s$,C错误,D正确。
规律总结
绳(杆)端速度分解模型
1.模型特点
两物体通过绳(杆)相连,当两物体都运动时,两物体的速度往往不相等,但因绳(杆)的长度是不变的,所以两物体的速度沿绳(杆)方向的分速度大小相等。
2.解题思路
先明确合运动(物体的实际运动)的方向,然后按运动的实际效果[一方面有沿绳(杆)方向伸缩的效果,另一方面有使绳(杆)转动的效果]确定两个分运动的方向:沿绳(杆)方向的分运动和垂直绳(杆)方向的分运动,而沿绳(杆)方向的分速度大小相等。
3.解决绳(杆)端速度分解问题的技巧
(1)明确分解谁:分解不沿绳(杆)方向运动物体的速度;
(2)知道如何分解:沿绳(杆)方向和垂直绳(杆)方向分解;
(3)求解依据:因为绳(杆)不能伸长,所以沿绳(杆)方向的速度分量大小相等。
9.ABD 本题主要考查关联速度 对P和Q的运动分解,如图所示

由关联速度可知$v_P\cos\alpha = v_Q\cos\beta$,则$v_Q = \frac{\cos\alpha}{\cos\beta}v_P$,当OP与OQ垂直时,$\alpha = \beta$,曲轴P速度的大小为$v_0$,可知活塞运动的速度等于P点的速度,都是$v_0 = 12m/s$,A正确;当O、P、Q在同一直线时,P点的速度方向与OQ方向垂直,沿OQ方向的分速度为零,Q的瞬时速度为零,所以活塞运动的速度等于零,B正确;当PQ垂直于OP时,即杆与圆相切,$v_Q = \frac{v_0}{\cos\beta}$,根据几何关系可得$\cos\beta = \frac{4}{5}$,解得$v_Q = 15m/s$,C错误,D正确。
规律总结
绳(杆)端速度分解模型
1.模型特点
两物体通过绳(杆)相连,当两物体都运动时,两物体的速度往往不相等,但因绳(杆)的长度是不变的,所以两物体的速度沿绳(杆)方向的分速度大小相等。
2.解题思路
先明确合运动(物体的实际运动)的方向,然后按运动的实际效果[一方面有沿绳(杆)方向伸缩的效果,另一方面有使绳(杆)转动的效果]确定两个分运动的方向:沿绳(杆)方向的分运动和垂直绳(杆)方向的分运动,而沿绳(杆)方向的分速度大小相等。
3.解决绳(杆)端速度分解问题的技巧
(1)明确分解谁:分解不沿绳(杆)方向运动物体的速度;
(2)知道如何分解:沿绳(杆)方向和垂直绳(杆)方向分解;
(3)求解依据:因为绳(杆)不能伸长,所以沿绳(杆)方向的速度分量大小相等。
查看更多完整答案,请扫码查看


