《2025年期中期末名校名区真题精编高一物理上册人教版》

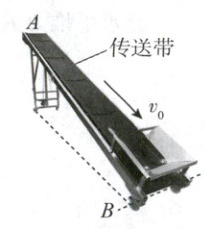
14. （12分）如图所示，快递站的工作人员利用传送带运送物品。传送带与水平面夹角θ = 37°，以恒定的速率v₀ = 5m/s沿顺时针向下转动，传送带两端A、B之间的距离为x = 4m，物品与传送带间的动摩擦因数为μ = 0.5。工作人员把物品从A端由静止释放，物品可视为质点，重力加速度g取10m/s²，sin37° = 0.6，cos37° = 0.8。求：
（1）物品刚放到传送带上时加速度的大小；
（2）物品通过传送带由A端到B端所用的时间。

答案： 14.
(1)$10 \ m/s^2$
(2)$1 \ s$
［解析］ 本题主要考查传送带模型
(1)物品刚放到传送带上时，由牛顿第二定律可得$\mu mg\cos 37^{\circ}+mg\sin 37^{\circ}=ma_1$解得加速度大小为$a_1=10 \ m/s^2$
(2)假设物品与传送带共速时未运动到$B$端，物品以加速度大小$a_1$做匀加速直线运动直至与传送带共速所用时间为$t_1=\frac{v_0}{a_1}=0.5 \ s$该过程物品通过的位移大小为$x_1=\frac{1}{2}a_1t_1^2=1.25 \ m＜x=4 \ m$故假设成立，由于$\mu＜\tan\theta$，共速后，设物品以加速度$a_2$继续做匀加速直线运动，根据牛顿第二定律可得$mg\sin 37^{\circ}-\mu mg\cos 37^{\circ}=ma_2$解得$a_2=2 \ m/s^2$
根据运动学公式可得$x-x_1=v_0t_2+\frac{1}{2}a_2t_2^2$解得$t_2=0.5 \ s$
则物品通过传送带由$A$端到$B$端所用的时间为$t=t_1+t_2=1 \ s$
模型总结
传送带向下传送物体问题的分类讨论
1.如图，若$0 \leq v_0＜v$且$\mu＞\tan\theta$：
(1)传送带比较短时，物块一直以$a=\mu g\cos\theta+g\sin\theta$向下匀加速运动。
(2)传送带足够长时，物块先以$a=\mu g\cos\theta+g\sin\theta$向下匀加速运动，再以速度$v$向下匀速运动。
2.若$0 \leq v_0＜v$且$\mu＜\tan\theta$：
(1)传送带比较短时，物块一直以$a=\mu g\cos\theta+g\sin\theta$向下匀加速运动。
(2)传送带足够长时，物块先以$a=\mu g\cos\theta+g\sin\theta$向下匀加速运动，再以$a=g\sin\theta-\mu g\cos\theta$向下匀加速运动。
3.若$v_0＞v$且$\mu＞\tan\theta$：
(1)传送带比较短时，物块一直以$a=\mu g\cos\theta-g\sin\theta$向下匀减速运动。
(2)传送带足够长时，物块先以$a=\mu g\cos\theta-g\sin\theta$向下匀减速运动，再以速度$v$向下匀速运动。
4.若$v_0＞v$且$\mu＜\tan\theta$：物块一直以$a=g\sin\theta-\mu g\cos\theta$向下匀加速运动。
技巧点拨
物块在倾斜传送带上的运动情形还有很多种，但分析思路大体相同：
(1)判断物块相对于传送带的运动方向，从而判断滑动摩擦力的方向。
(2)列牛顿第二定律方程，分析加速度$a$的方向和大小。
(3)根据临界条件$v_{物}=v_{带}$确定临界状态的运动情况，根据$\mu$与$\tan\theta$的大小关系判断物块之后的运动情形。