第53页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
11. 【原创题】如图,在 $ 3 × 3 $ 的正方形网格中有四个格点 $ A,B,C,D $,以其中一个点为原点,网格线所在直线为坐标轴,建立平面直角坐标系,使其余三个点中存在两个点关于一条坐标轴对称,则原点可能是(
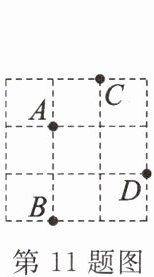
A.点 $ A $
B.点 $ B $
C.点 $ C $
D.点 $ D $
D
)
A.点 $ A $
B.点 $ B $
C.点 $ C $
D.点 $ D $
答案:
D
12. 如图,在平面直角坐标系中,$\triangle ABC$ 关于直线 $ m $(直线 $ m $ 上各点的横坐标都为 $ 1 $)对称,点 $ B $ 的坐标为 $(-2,1)$,则点 $ C $ 的坐标为______.
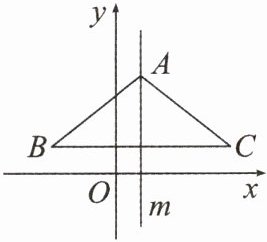

(4,1)
答案:
(4,1)
13. 如图,小李同学在学习完平面直角坐标系后,在直角坐标系中画了一只可爱的“小猫”.
(1)请在这个直角坐标系中再画一只“小猫”,使得新画的“小猫”与原图案关于 $ y $ 轴对称;
(2)分别写出新图案“小猫”耳尖位置点 $ A',B' $ 的坐标.(点 $ A' $ 与点 $ A $ 对应,点 $ B' $ 与点 $ B $ 对应)
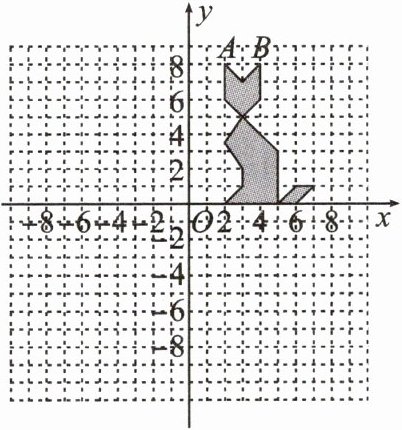
(1)请在这个直角坐标系中再画一只“小猫”,使得新画的“小猫”与原图案关于 $ y $ 轴对称;
(2)分别写出新图案“小猫”耳尖位置点 $ A',B' $ 的坐标.(点 $ A' $ 与点 $ A $ 对应,点 $ B' $ 与点 $ B $ 对应)

答案:
(1)解:如图所示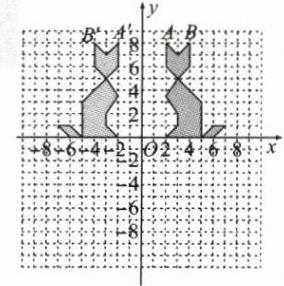
(2)由图可知,新图案“小猫”耳尖位置点A',B'的坐标分别为(-2,8),(-4,8).
(1)解:如图所示

(2)由图可知,新图案“小猫”耳尖位置点A',B'的坐标分别为(-2,8),(-4,8).
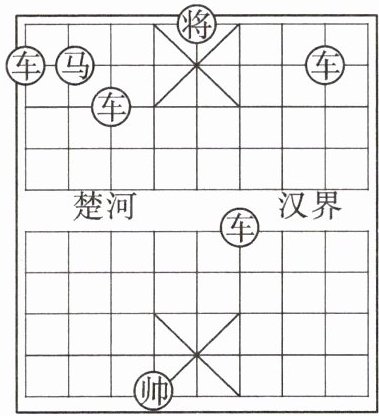
14. 【新课标·传统文化】为参加学校举办的象棋大赛,小明和小华在课余时间进行棋艺切磋,棋局如下. 若“将”的坐标为 $(0,5)$,“马”的坐标为 $(-3,4)$.
(1)在棋盘上画出平面直角坐标系,并写出“帅”的坐标;
(2)棋盘中有一个“车”和“马”关于 $ y $ 轴对称,求这个“车”和“马”“将”组成的三角形的面积.
(1)在棋盘上画出平面直角坐标系,并写出“帅”的坐标;
(2)棋盘中有一个“车”和“马”关于 $ y $ 轴对称,求这个“车”和“马”“将”组成的三角形的面积.

答案:
(1)解:建立平面直角坐标系如图所示! ,“帅”的坐标为(-1,-4);
,“帅”的坐标为(-1,-4);
(2)
∵棋盘有一个“车”和“马”关于y轴对称,
∴此“车”的坐标为(3,4),
∴这个“车”和“马”“将”组成的三角形的面积为12×6×1=3.
(1)解:建立平面直角坐标系如图所示!
 ,“帅”的坐标为(-1,-4);
,“帅”的坐标为(-1,-4);(2)
∵棋盘有一个“车”和“马”关于y轴对称,
∴此“车”的坐标为(3,4),
∴这个“车”和“马”“将”组成的三角形的面积为12×6×1=3.
查看更多完整答案,请扫码查看


