第48页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
9. 如图,已知线段AB,BC的垂直平分线$l_1,l_2$交于点M,则线段AM,CM的大小关系是(
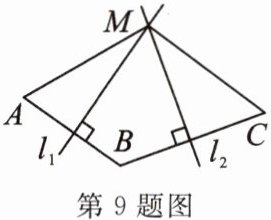
A.AM>CM
B.AM= CM
C.AM<CM
D.无法确定
B
)
A.AM>CM
B.AM= CM
C.AM<CM
D.无法确定
答案:
B
10. 如图,△ABC中,∠B= 40°,AC的垂直平分线交AC于点D,交BC于点E,且∠EAB:∠CAE= 3:1,则∠C等于
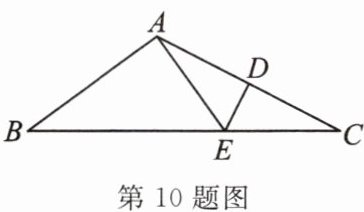
28
度.
答案:
28
11. (教材第67页第3题变式)写出下列命题的逆命题,并判断这些逆命题是否成立.
(1)直角三角形的两个锐角互余;
(2)如果a的值大于b,那么a的绝对值也大于b.
(1)直角三角形的两个锐角互余;
(2)如果a的值大于b,那么a的绝对值也大于b.
答案:
(1)解:有两个锐角互余的三角形是直角三角形.成立. (2)如果a的绝对值大于b,那么a的值也大于b.不成立.
12. 如图,P是∠AOB平分线上的一点,PD⊥OA,PE⊥OB,垂足分别为D,E,连接DE. 求证:
(1)OD= OE;
(2)OP垂直平分DE.
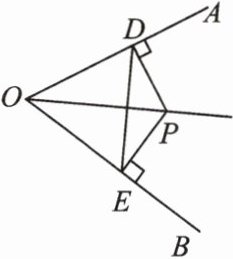
(1)OD= OE;
(2)OP垂直平分DE.

答案:
(1)证明:
∵P是∠AOB平分线上的一点,PD⊥OA,PE⊥OB,
∴PD=PE.在Rt△ODP和Rt△OEP中,{OP=OP,PD=PE,
∴Rt△ODP≌Rt△OEP(HL),
∴OD=OE. (2)
∵DP=PE,OD=OE,
∴OP是DE的垂直平分线,即OP垂直平分DE.
∵P是∠AOB平分线上的一点,PD⊥OA,PE⊥OB,
∴PD=PE.在Rt△ODP和Rt△OEP中,{OP=OP,PD=PE,
∴Rt△ODP≌Rt△OEP(HL),
∴OD=OE. (2)
∵DP=PE,OD=OE,
∴OP是DE的垂直平分线,即OP垂直平分DE.
13. 【核心素养·推理能力】如图,在锐角三角形ABC中,AB,AC边的垂直平分线交于点O,∠BAC= α(0°<α<90°).
(1)求∠BOC的度数;
(2)试判断∠ABO+∠ACB是否为定值?若是,求出此定值;若不是,请说明理由.
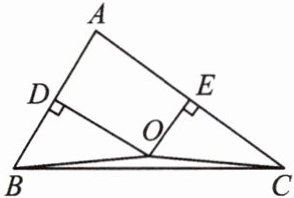
(1)求∠BOC的度数;
(2)试判断∠ABO+∠ACB是否为定值?若是,求出此定值;若不是,请说明理由.

答案:
(1)解:连接AO.
∵AB,AC边的垂直平分线交于点O,易证△BDO≌△ADO及△AEO≌△CEO或由对称性得∠OAB=∠OBA,∠OCA=∠OAC.
∴∠AOB+∠AOC=(180°-∠OAB-∠OBA)+(180°-∠OAC-∠OCA)=(180°-2∠OAB)+(180°-2∠OAC)=360°-2(∠OAB+∠OAC)=360°-2∠BAC=360°-2α.
∴∠BOC=360°-(∠AOB+∠AOC)=2α.
(2)∠ABO+∠ACB为定值.由BO=CO,易证∠OBC=∠OCB.
∵∠BOC=2α,
∴∠OBC=1/2(180°-2α)=90°-α.
∵∠ABO+∠ACB+∠OBC+∠BAC=180°,
∴∠ABO+∠ACB=180°-α-(90°-α)=90°.
∵AB,AC边的垂直平分线交于点O,易证△BDO≌△ADO及△AEO≌△CEO或由对称性得∠OAB=∠OBA,∠OCA=∠OAC.
∴∠AOB+∠AOC=(180°-∠OAB-∠OBA)+(180°-∠OAC-∠OCA)=(180°-2∠OAB)+(180°-2∠OAC)=360°-2(∠OAB+∠OAC)=360°-2∠BAC=360°-2α.
∴∠BOC=360°-(∠AOB+∠AOC)=2α.
(2)∠ABO+∠ACB为定值.由BO=CO,易证∠OBC=∠OCB.
∵∠BOC=2α,
∴∠OBC=1/2(180°-2α)=90°-α.
∵∠ABO+∠ACB+∠OBC+∠BAC=180°,
∴∠ABO+∠ACB=180°-α-(90°-α)=90°.
查看更多完整答案,请扫码查看


