《2025年新课标学习方法指导丛书七年级数学上册浙教版》

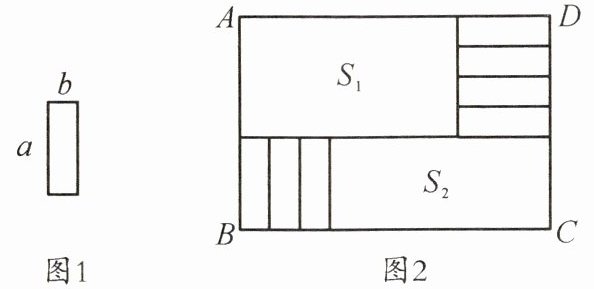
12. 将7张相同的小长方形纸片(如图1所示),按图2所示的方式不重叠地放在长方形$ABCD$内,未被覆盖的部分恰好被分割为两个长方形,面积分别为$S_{1}$,$S_{2}$,已知小长方形纸片的长为$a$,宽为$b$,且$a＞b$。

(1)当$a= 7$,$b= 2$,$AD= 30$时,求长方形$ABCD$的面积。
(2)当$AD= 30$时,请用含$a$,$b的式子表示S_{1}-S_{2}$的值。
(3)若$AB$长度不变,$AD$变长,将这7张小长方形纸片还按照同样的方式放在新的长方形$ABCD$内,且$S_{1}-S_{2}$的值保持不变,则$a$,$b$满足的关系式是______。

答案： 解:
(1)长方形 $ABCD$ 的面积为 $30×(4×2 + 7)=450$。
(2)$S_{1}-S_{2}=4b(30 - a)-a(30 - 3b)$
$=120b - 4ab - 30a + 3ab$
$=120b - ab - 30a$。
(3)$S_{1}-S_{2}=4b(AD - a)-a(AD - 3b)$，
整理，得 $S_{1}-S_{2}=(4b - a)AD - ab$。
因为 $S_{1}-S_{2}$ 的值总保持不变，即 $S_{1}-S_{2}$ 的值与 $AD$ 的值无关，
所以 $4b - a = 0$，
解得 $a = 4b$。
故答案为 $a = 4b$。

13. 阅读材料,回答问题。
我们知道,$4x-2x+x= (4-2+1)x= 3x$,类似地,我们把$(a+b)$看成一个整体,则$4(a+b)-2(a+b)+(a+b)= (4-2+1)(a+b)= 3(a+b)$。“整体思想”是初中数学解题中的一种重要的思想方法,它在多项式的化简与求值中应用极为广泛。
(1)把$(a-b)^{2}$看成一个整体,合并$2(a-b)^{2}-6(a-b)^{2}+3(a-b)^{2}$。
(2)已知$x^{2}-2y= 4$,求$6x^{2}-12y-27$的值。
(3)已知$a-2b= 3$,$2b-c= -5$,$c-d= 10$,求$(a-c)+(2b-d)-(2b-c)$的值。

答案：
(1)
$2(a-b)^{2} - 6(a-b)^{2} + 3(a-b)^{2}$
$= (2 - 6 + 3)(a-b)^{2}$
$= -1(a-b)^{2}$
$= -(a-b)^{2}$
(2)
因为 $x^{2} - 2y = 4$，
所以 $6x^{2} - 12y - 27$
$= 6(x^{2} - 2y) - 27$
$= 6 × 4 - 27$
$= 24 - 27$
$= -3$
(3)
因为 $a - 2b = 3$，$2b - c = -5$，$c - d = 10$，
所以 $a - c = (a - 2b) + (2b - c) = 3 + (-5) = -2$，
$2b - d = (2b - c) + (c - d) = -5 + 10 = 5$，
$(a-c) + (2b-d) - (2b-c)$
$= -2 + 5 - (-5)$
$= -2 + 5 + 5$
$= 8$