《2025年新课标学习方法指导丛书七年级数学上册浙教版》

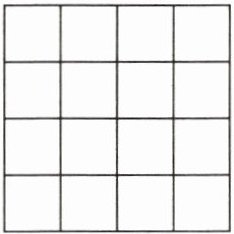
13. 在如图$4×4$的正方形网格图中,每个小正方形的边长都为1,请在图中画出一条长为$\sqrt {10}$的线段。

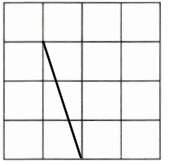
答案：

14. 大家知道,$\sqrt {3}$是无理数,而无理数是无限不循环小数,因此$\sqrt {3}$的小数部分我们不可能全部写出来,于是李峰同学用$\sqrt {3}-1来表示\sqrt {3}$的小数部分,李峰同学的表示方法对吗？
事实上,李峰同学的表示方法是有道理的,因为$\sqrt {3}$的整数部分是1,将$\sqrt {3}$减去其整数部分,差就是其小数部分。
请解答下面的问题：已知$12+\sqrt {6}= a+b$,a是$12+\sqrt {6}$的整数部分,b是$12+\sqrt {6}$的小数部分,求$a-b$的相反数。

答案： 首先确定$\sqrt{6}$的范围：
因为$2^2 = 4 ＜ 6$ 且 $3^2 = 9 ＞ 6$，
所以$2 ＜ \sqrt{6} ＜ 3$。
接着确定$12 + \sqrt{6}$的范围：
$14 ＜ 12 + \sqrt{6} ＜ 15$，
确定$a$和$b$的值：
整数部分$a = 14$，
小数部分$b = 12 + \sqrt{6} - 14 = \sqrt{6} - 2$。
计算$a - b$：
$a - b = 14 - (\sqrt{6} - 2) = 16 - \sqrt{6}$。
求$a - b$的相反数：
$-(a - b) = - (16 - \sqrt{6}) = \sqrt{6} - 16$。
故答案为：$\sqrt{6} - 16$。