《2025年新课标学习方法指导丛书七年级数学上册浙教版》

13. 如图1,现有三种边长分别为3,2,1的正方形卡片,分别记为Ⅰ,Ⅱ,Ⅲ,还有一个长为$a$,宽为$b$的长方形。

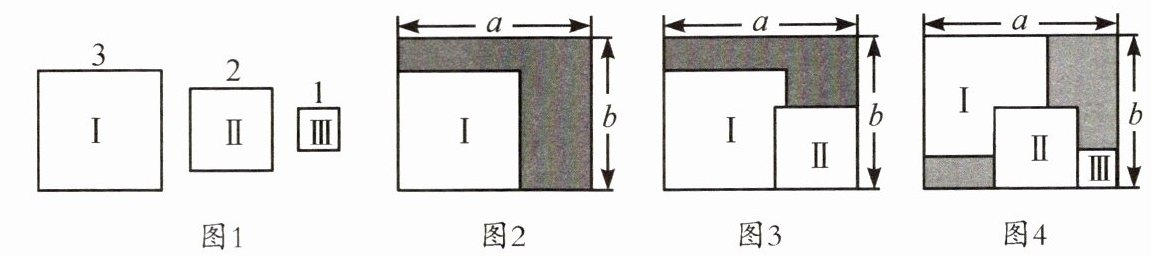
(1)如图2,将正方形卡片Ⅰ放置在长方形中,试用含$a,b$的代数式表示阴影部分的面积,并求当$a= 4.5,b= 4$时阴影部分的面积。
(2)将Ⅰ,Ⅱ两张正方形卡片按图3的方式放置在长方形中,试用含$a,b$的代数式表示阴影部分的面积,并求当$a= 4.5,b= 4$时阴影部分的面积。
(3)将Ⅰ,Ⅱ,Ⅲ三张正方形卡片按图4的方式放置在长方形中,求右上角阴影部分与左下角阴影部分周长的差。

答案：

解：

(1) $ S_{阴}=ab - 9 $，当 $ a = 4.5 $，$ b = 4 $ 时，

$ S_{阴}=4.5×4 - 9 = 18 - 9 = 9 $；

(2) $ S_{阴}=ab - 9 - 2(a - 3)=ab - 2a - 3 $，

当 $ a = 4.5 $，$ b = 4 $ 时，

$ S_{阴}=4.5×4 - 2×4.5 - 3 = 6 $；

(3) 周长之差为：

$\begin{aligned}&2(a - 3)+2(b - 1)-[2(a - 3)+2(b - 3)]\\=&2a - 6 + 2b - 2-(2a - 6 + 2b - 6)\\=&2a + 2b - 8 - 2a - 2b + 12\\=&4.\end{aligned}$

故右上角阴影部分与左下角阴影部分周长的差为 $ 4 $。