《2025年学习与评价江苏教育出版社九年级数学上册苏科版》

1. 选择题：
(1)下列说法中,正确的是(B).
A.弦是直径
B.半圆是弧
C.过圆心的线段是直径
D.圆心相同、半径相同的两个圆是同心圆

答案： 【解析】：
本题主要考查了圆的基本概念，包括弦、直径、弧、同心圆等定义。
A选项：弦是连接圆上任意两点的线段，而直径是特殊的弦，它通过圆心。但不是所有的弦都是直径，所以A选项错误。
B选项：半圆实际上是圆上的一段弧，它恰好占据了圆的一半。因此，半圆确实是一种特殊的弧，B选项正确。
C选项：虽然直径是过圆心的线段，但并非所有过圆心的线段都是直径。直径还需要连接圆上的两点，所以C选项错误。
D选项：同心圆的定义是有共同圆心但半径不同的圆。题目中说的是“圆心相同、半径相同”，这实际上描述的是同一个圆，而不是同心圆，所以D选项错误。
综上所述，只有B选项是正确的。
【答案】：
B

(2)依次连接圆内两条相交直径的4个端点,围成的四边形一定是(C).
A.梯形
B.菱形
C.矩形
D.正方形

答案： 解：设圆的两条相交直径为AC和BD，交点为圆心O。
因为AC和BD是圆的直径，所以OA=OC=OB=OD。
所以四边形ABCD的对角线互相平分且相等。
根据矩形的判定定理：对角线互相平分且相等的四边形是矩形。
所以四边形ABCD一定是矩形。
答案：C

(3)下列说法中,正确的是(B).
A.两个半圆是等弧
B.同圆中优弧与半圆的差必是劣弧
C.长度相等的弧是等弧
D.直径未必是弦

答案： 【解析】：
本题主要考察圆的基本概念，包括半圆、优弧、劣弧、等弧以及弦的定义。
A选项：两个半圆是等弧。这个说法是不准确的，因为等弧的定义是在同一个圆或等圆中，能够互相重合的弧。而两个半圆不一定在同一个圆中，因此不能说两个半圆就是等弧。
B选项：同圆中优弧与半圆的差必是劣弧。这个说法是正确的。在同圆中，优弧是长度大于半圆的弧，那么优弧减去半圆后的弧长必然小于半圆，即为劣弧。
C选项：长度相等的弧是等弧。这个说法是不准确的。等弧不仅要求长度相等，还要求在同一个圆或等圆中能够互相重合。
D选项：直径未必是弦。这个说法是不准确的。根据弦的定义，连接圆上任意两点的线段叫做弦。直径是连接圆上两点且经过圆心的特殊弦，因此直径一定是弦。
综上所述，只有B选项是正确的。
【答案】：
B

2. 填空题：
(1)已知圆内一点P到圆周上的点的最长距离是7 cm,最短距离是3 cm,此圆的半径是5cm.

答案： 5
4

(2)如图,AB是⊙O的直径,D是弦BC的中点.已知OD= 2 cm,则弦AC= ______cm.

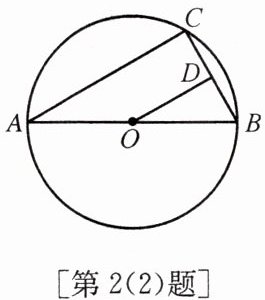
4

答案： 解：
∵AB是⊙O的直径，
∴O是AB的中点。
∵D是弦BC的中点，
∴OD是△ABC的中位线。
∴AC=2OD。
∵OD=2cm，
∴AC=2×2=4cm。
4

3. 如图,两个同心圆的圆心为O,大圆的半径OA、OB分别交小圆于点C、D,连接AD、BC.
求证：AD= BC.

答案： 证明：由圆的性质可知OA=OB、OC=OD
在△AOD和△BOC中
$ \begin{cases}OA=OB\\∠AOD=∠BOC\\OD=OC\end{cases}$
∴$△AOD≌△BOC(\mathrm {SAS})$
∴AD=BC