第39页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
2. 选择题:
(1)圆是轴对称图形,它的对称轴有(
A. 1条
B. 2条
C. 4条
D. 无数条
(2)"圆材埋壁"是我国古代著名的数学著作《九章算术》中的一个问题:"今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?"用现在的数学语言表述是:"如图,CD为$\odot O$的直径,弦$AB\perp CD$,垂足为E,$CE= 1$寸,$AB= 10$寸,求直径CD的长."根据题意,CD长为(
A. $\frac{25}{2}$寸
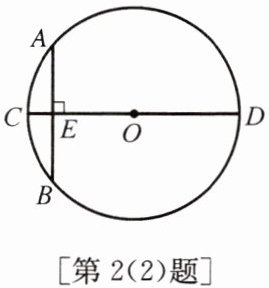
B. 13寸
C. 25寸
D. 26寸
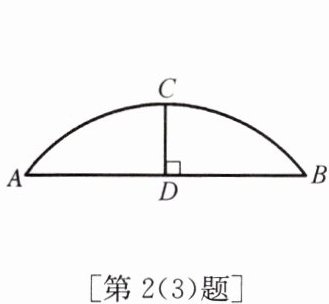
(3)一种花边是由如图的弓形组成的,$\overset{\frown}{ACB}$的所在圆的半径为5,弦$AB= 8$,则弓形的高(弧的中点到弦的距离)CD的长为(
A. 2
B. $\frac{5}{2}$
C. 3
D. $\frac{16}{3}$
(1)圆是轴对称图形,它的对称轴有(
D
).A. 1条
B. 2条
C. 4条
D. 无数条
(2)"圆材埋壁"是我国古代著名的数学著作《九章算术》中的一个问题:"今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?"用现在的数学语言表述是:"如图,CD为$\odot O$的直径,弦$AB\perp CD$,垂足为E,$CE= 1$寸,$AB= 10$寸,求直径CD的长."根据题意,CD长为(
D
).A. $\frac{25}{2}$寸


B. 13寸
C. 25寸
D. 26寸
(3)一种花边是由如图的弓形组成的,$\overset{\frown}{ACB}$的所在圆的半径为5,弦$AB= 8$,则弓形的高(弧的中点到弦的距离)CD的长为(
A
).A. 2
B. $\frac{5}{2}$
C. 3
D. $\frac{16}{3}$
答案:
D
D
A
D
A
3. 如图,$\odot O的半径OC= 6$,弦AB垂直平分OC.求弦AB的长.
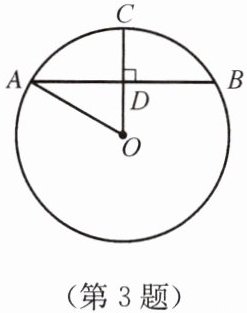

答案:
解:
∵AB垂直平分OC
∴CD=OD=3
在Rt△ADO中,AO=6,OD=3
∴$ AD=\sqrt{AO^2-OD^2}=3\sqrt{3}$
∵OC⊥AB
∴$ AB=2AD=6\sqrt{3}$
∵AB垂直平分OC
∴CD=OD=3
在Rt△ADO中,AO=6,OD=3
∴$ AD=\sqrt{AO^2-OD^2}=3\sqrt{3}$
∵OC⊥AB
∴$ AB=2AD=6\sqrt{3}$
4. 如图,将一个两边都带有刻度的直尺放在半圆形纸片上,使其一边经过圆心O,另一边所在直线与半圆相交于点D、E,量出半径$OC= 5\ cm$,弦$DE= 8\ cm$.求直尺的宽.
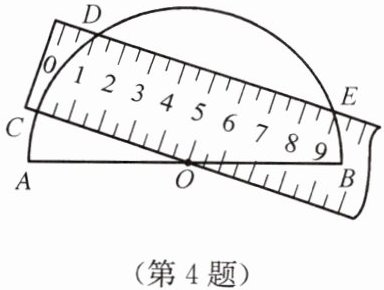

答案:
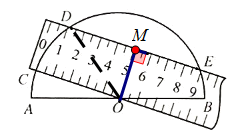
解:过点O作OM⊥DE,垂足为点M,连接OD
∴$ DM=\frac 12DE$
∵$DE=8\ \mathrm {cm}$
∴$DM=4\ \mathrm {cm}$
在Rt△ODM中,$OD=DC=5\ \mathrm {cm}$
∴$ OM=\sqrt{OD^2-DM^2}=\sqrt{5^{2}-4^{2}}=3\ \mathrm {cm}$
则直尺的宽为$3\ \mathrm {cm}$

解:过点O作OM⊥DE,垂足为点M,连接OD
∴$ DM=\frac 12DE$
∵$DE=8\ \mathrm {cm}$
∴$DM=4\ \mathrm {cm}$
在Rt△ODM中,$OD=DC=5\ \mathrm {cm}$
∴$ OM=\sqrt{OD^2-DM^2}=\sqrt{5^{2}-4^{2}}=3\ \mathrm {cm}$
则直尺的宽为$3\ \mathrm {cm}$
查看更多完整答案,请扫码查看


