《2025年学习与评价江苏教育出版社九年级数学上册苏科版》

7. 如图,$\widehat{AB}的长度是\widehat{CD}$的长度的2倍.弦AB的长度是弦CD的长度的2倍吗？动手量一量,并说明其中的道理.

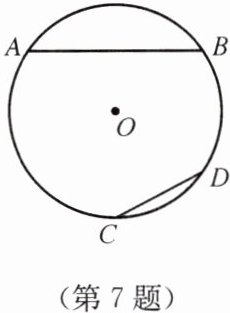
答案： 解：AB<2CD
理由： 取$\widehat{AB}$的中点E，连接AE、BE
∵$ \widehat{AB}=2\widehat{CD}$
∴$ \widehat{AE}=\widehat{BE}=\widehat{CD}$
∴AE=BE=CD
在△AEB中，AE+BE>AB
∴2CD>AB

如图2-7,剪一个圆形纸片,对折后使两个半圆完全重合,重复做几次,你发现了什么？由此你能得到什么结论？

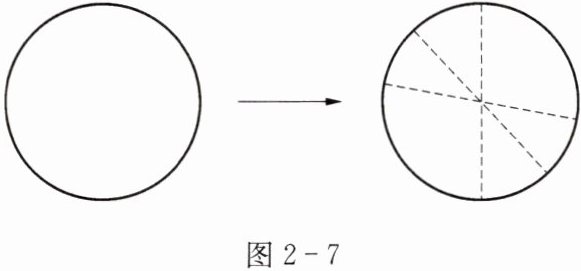
答案： 解：实验表明，直径两侧的半圆能互相重合，
这说明圆是轴对称图形
结论：经过圆心的每一条直线都是对称轴

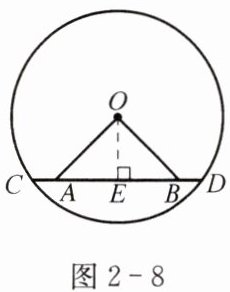
例1 如图2-8,在$\odot O$中,点A、B在弦CD上,且$OA= OB$.
求证:$AC= BD$.
证明 过圆心O作$OE\perp AB$,垂足为E,则$CE= ED$.
$\because OA= OB$,
$\therefore AE= BE$.
$\therefore AC= BD$.
说明 若将A、B视为弦CD上的两动点,则在变化过程中,只要满足一组对称的变化,那么根据其轴对称性均可得到其他对称的结果,"过点O作弦的垂线"为关键点.

答案： 证明：过圆心O作OE⊥CD，垂足为E，
∵OE过圆心且OE⊥CD，
∴CE=ED（垂直于弦的直径平分弦）。
∵OA=OB，OE⊥AB（CD与AB共线，OE⊥CD即OE⊥AB），
∴AE=BE（等腰三角形底边上的高平分底边）。
∵CE=ED，AE=BE，
∴CE - AE = ED - BE，即AC=BD。

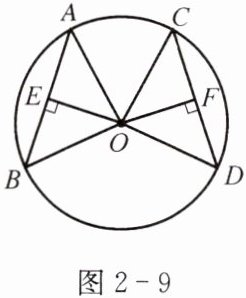
例2 如图2-9,在$\odot O$中,AB、CD是两条弦,$OE\perp AB$,$OF\perp CD$,垂足分别为E、F.
(1)已知$\angle AOB= \angle COD$,那么OE与OF的大小有什么关系?为什么?
(2)已知$OE= OF$,那么AB与CD的大小有什么关系?$\overset{\frown}{AB}与\overset{\frown}{CD}$的大小有什么关系?为什么?$\angle AOB与\angle COD$呢?
解 (1)$OE= OF$.理由：
$\because \angle AOB= \angle COD$,
$\therefore AB= CD$.
$\because OE\perp AB$,$OF\perp CD$,
$\therefore AE= \frac{1}{2}AB$,$CF= \frac{1}{2}CD$.
$\therefore AE= CF$.
又$\because OA= OC$,
$\therefore Rt\triangle OAE\cong Rt\triangle OCF$.
$\therefore OE= OF$.
(2)$AB= CD$,$\overset{\frown}{AB}= \overset{\frown}{CD}$,$\angle AOB= \angle COD$.理由：
$\because OE\perp AB$,$OF\perp CD$,
$\therefore AE= \frac{1}{2}AB$,$CF= \frac{1}{2}CD$.
$\because OA= OC$,$OE= OF$,
$\therefore Rt\triangle OAE\cong Rt\triangle OCF$.
$\therefore AE= CF$.
$\therefore AB= CD$.
$\therefore \overset{\frown}{AB}= \overset{\frown}{CD}$,$\angle AOB= \angle COD$.
说明 我们可以看出：在同圆或等圆中,如果两个圆心角、两条弧、两条弦或圆心到这两条弦的距离中有一组量相等,那么它们所对应的其余各组量都分别相等.

答案：
(1)$OE=OF$.理由：
$\because\angle AOB=\angle COD$,
$\therefore AB=CD$.
$\because OE\perp AB$,$OF\perp CD$,
$\therefore AE=\frac{1}{2}AB$,$CF=\frac{1}{2}CD$.
$\therefore AE=CF$.
又$\because OA=OC$,
$\therefore Rt\triangle OAE\cong Rt\triangle OCF$.
$\therefore OE=OF$.
(2)$AB=CD$,$\overset{\frown}{AB}=\overset{\frown}{CD}$,$\angle AOB=\angle COD$.理由：
$\because OE\perp AB$,$OF\perp CD$,
$\therefore AE=\frac{1}{2}AB$,$CF=\frac{1}{2}CD$.
$\because OA=OC$,$OE=OF$,
$\therefore Rt\triangle OAE\cong Rt\triangle OCF$.
$\therefore AE=CF$.
$\therefore AB=CD$.
$\therefore\overset{\frown}{AB}=\overset{\frown}{CD}$,$\angle AOB=\angle COD$.