第84页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
2. 某地连续统计了10天的日最高气温,并绘制成如图所示的扇形统计图.
(1)这10天中,日最高气温的众数是
(2)求这10天日最高气温的平均值.
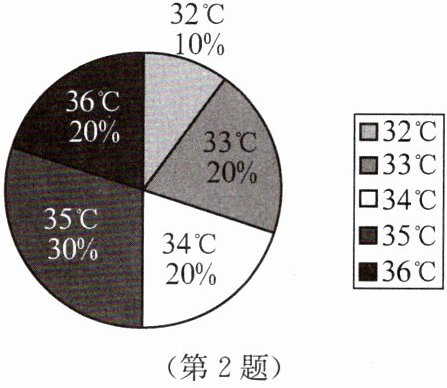
(2)解:32×10%×10=32×1=32
33×20%×10=33×2=66
34×20%×10=34×2=68
35×30%×10=35×3=105
36×20%×10=36×2=72
(32+66+68+105+72)÷10=343÷10=34.3
答:这10天日最高气温的平均值为34.3℃。
(1)这10天中,日最高气温的众数是
35
℃,中位数是34.5
℃;(2)求这10天日最高气温的平均值.

(2)解:32×10%×10=32×1=32
33×20%×10=33×2=66
34×20%×10=34×2=68
35×30%×10=35×3=105
36×20%×10=36×2=72
(32+66+68+105+72)÷10=343÷10=34.3
答:这10天日最高气温的平均值为34.3℃。
答案:
(1)35,34.5
(2)解:32×10%×10=32×1=32
33×20%×10=33×2=66
34×20%×10=34×2=68
35×30%×10=35×3=105
36×20%×10=36×2=72
(32+66+68+105+72)÷10=343÷10=34.3
答:这10天日最高气温的平均值为34.3℃。
(1)35,34.5
(2)解:32×10%×10=32×1=32
33×20%×10=33×2=66
34×20%×10=34×2=68
35×30%×10=35×3=105
36×20%×10=36×2=72
(32+66+68+105+72)÷10=343÷10=34.3
答:这10天日最高气温的平均值为34.3℃。
3. 在什么情况下,众数可以帮助人们更好地进行决策?请举一个例子说明.
答案:
【解析】:
本题主要考察众数的概念及其在实际问题中的应用。众数是一组数据中出现次数最多的数值。在决策过程中,众数可以帮助我们了解大多数人的选择或偏好,从而作出更符合大众需求的决策。例如,在市场营销中,了解哪种产品最受欢迎(即销售量最大的产品),可以帮助商家决定生产哪种产品以满足市场需求。
【答案】:
当需要了解大多数人的选择或偏好以进行决策时,众数可以帮助人们更好地进行决策。例如,一个服装品牌商想要决定下一季主打哪种款式的衣服,他可以通过销售数据分析,找到销售量最大的款式(即众数),从而决定生产更多这种款式的衣服以满足市场需求。
本题主要考察众数的概念及其在实际问题中的应用。众数是一组数据中出现次数最多的数值。在决策过程中,众数可以帮助我们了解大多数人的选择或偏好,从而作出更符合大众需求的决策。例如,在市场营销中,了解哪种产品最受欢迎(即销售量最大的产品),可以帮助商家决定生产哪种产品以满足市场需求。
【答案】:
当需要了解大多数人的选择或偏好以进行决策时,众数可以帮助人们更好地进行决策。例如,一个服装品牌商想要决定下一季主打哪种款式的衣服,他可以通过销售数据分析,找到销售量最大的款式(即众数),从而决定生产更多这种款式的衣服以满足市场需求。
4. 在课本习题3.1中,有这样一道题:
某手表厂抽查了100只手表的日走时误差,数据如下(单位:s):
|日走时误差|-2|-1|0|1|2|3|4|
|只数|3|10|18|28|20|16|5|
求这100只手表的日平均走时误差.
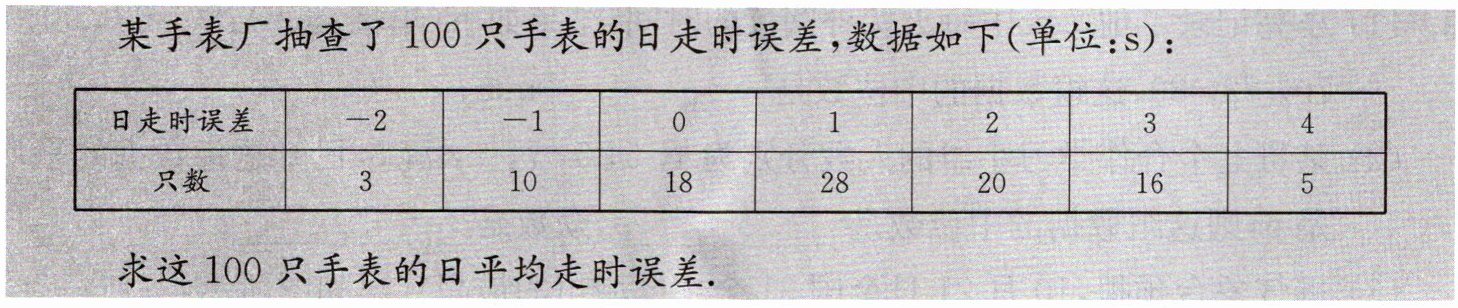
请你写出这100只手表的日走时误差的中位数和众数.
某手表厂抽查了100只手表的日走时误差,数据如下(单位:s):
|日走时误差|-2|-1|0|1|2|3|4|
|只数|3|10|18|28|20|16|5|
求这100只手表的日平均走时误差.

请你写出这100只手表的日走时误差的中位数和众数.
答案:
【解析】:本题考查平均数,中位数和众数的概念及其求解方法。
平均数是指在一组数据中所有数据之和再除以数据的个数。
中位数是按顺序排列的一组数据中居于中间位置的数,如果在数据集中有奇数个数据,则中位数是中间的那个数;如果有偶数个数据,中位数是中间两个数的平均值。
众数是一组数据中出现次数最多的数值。
根据平均数的计算公式,把这100只手表的日走时误差加起来,再除以100即可求出平均数。
中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(如果数据个数是奇数)或者最中间两个数的平均数(如果数据个数是偶数)。
众数是一组数据中出现次数最多的数据,找出这组数据中出现次数最多的数据即可。
【答案】:平均数:
$\frac{(-2)×3+(-1)×10+0×18+1×28+2×20+3×16+4×5}{100}$
$=\frac{-6-10+0+28+40+48+20}{100}$
$=\frac{120}{100}$
$=1.2(s)$
这100只手表的日平均走时误差是$1.2s$。
数据总数为100(偶数),按从小到大排列后,第50和第51个数据都是1(因为$3+10+18=31$,前31个数据是-2,-1,0,第32到59个数据是1),所以中位数是$\frac{1+1}{2}=1(s)$。
众数是出现次数最多的数,从表格中可以看出,日走时误差为1的只数最多(28只),所以众数是1s。
综上,这100只手表的日平均走时误差是$1.2s$,中位数是$1s$,众数是$1s$。
平均数是指在一组数据中所有数据之和再除以数据的个数。
中位数是按顺序排列的一组数据中居于中间位置的数,如果在数据集中有奇数个数据,则中位数是中间的那个数;如果有偶数个数据,中位数是中间两个数的平均值。
众数是一组数据中出现次数最多的数值。
根据平均数的计算公式,把这100只手表的日走时误差加起来,再除以100即可求出平均数。
中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(如果数据个数是奇数)或者最中间两个数的平均数(如果数据个数是偶数)。
众数是一组数据中出现次数最多的数据,找出这组数据中出现次数最多的数据即可。
【答案】:平均数:
$\frac{(-2)×3+(-1)×10+0×18+1×28+2×20+3×16+4×5}{100}$
$=\frac{-6-10+0+28+40+48+20}{100}$
$=\frac{120}{100}$
$=1.2(s)$
这100只手表的日平均走时误差是$1.2s$。
数据总数为100(偶数),按从小到大排列后,第50和第51个数据都是1(因为$3+10+18=31$,前31个数据是-2,-1,0,第32到59个数据是1),所以中位数是$\frac{1+1}{2}=1(s)$。
众数是出现次数最多的数,从表格中可以看出,日走时误差为1的只数最多(28只),所以众数是1s。
综上,这100只手表的日平均走时误差是$1.2s$,中位数是$1s$,众数是$1s$。
5. 小强是学校篮球队队员,他在最近5场比赛中的得分分别为10分、13分、9分、8分、10分.若小强下一场比赛得分是16分,则小强得分的三个统计量(平均数、中位数与众数)哪些发生了改变?改变后分别是多少?
答案:
【解析】:
本题考查统计量的计算,涉及到平均数、中位数和众数的概念。
首先我们计算原始数据(小强前5场比赛的得分)的平均数、中位数和众数。
然后,我们将下一场比赛的得分(16分)加入到数据集中,并重新计算平均数、中位数和众数。
最后,我们比较改变前后的统计量,找出哪些发生了改变,并给出改变后的具体数值。
原始数据:$10, 13, 9, 8, 10$
1. 平均数:
$平均数 = \frac{10 + 13 + 9 + 8 + 10}{5} = 10$
2. 中位数:
数据排序后为 $8, 9, 10, 10, 13$,中位数为 $10$。
3. 众数:
出现次数最多的数是 $10$,因此众数为 $10$。
加入新数据(16分)后的数据集:$10, 13, 9, 8, 10, 16$
1. 平均数:
$新平均数 = \frac{10 + 13 + 9 + 8 + 10 + 16}{6} = 11$
2. 中位数:
数据排序后为 $8, 9, 10, 10, 13, 16$,因为有6个数据点,中位数为 $\frac{10 + 10}{2} = 10$,中位数未改变。
3. 众数:
出现次数最多的数仍然是 $10$,因此众数未改变。
【答案】:
平均数发生了改变,改变后的平均数是 $11$ 分。
中位数没有发生改变,仍然是 $10$ 分。
众数没有发生改变,仍然是 $10$ 分。
本题考查统计量的计算,涉及到平均数、中位数和众数的概念。
首先我们计算原始数据(小强前5场比赛的得分)的平均数、中位数和众数。
然后,我们将下一场比赛的得分(16分)加入到数据集中,并重新计算平均数、中位数和众数。
最后,我们比较改变前后的统计量,找出哪些发生了改变,并给出改变后的具体数值。
原始数据:$10, 13, 9, 8, 10$
1. 平均数:
$平均数 = \frac{10 + 13 + 9 + 8 + 10}{5} = 10$
2. 中位数:
数据排序后为 $8, 9, 10, 10, 13$,中位数为 $10$。
3. 众数:
出现次数最多的数是 $10$,因此众数为 $10$。
加入新数据(16分)后的数据集:$10, 13, 9, 8, 10, 16$
1. 平均数:
$新平均数 = \frac{10 + 13 + 9 + 8 + 10 + 16}{6} = 11$
2. 中位数:
数据排序后为 $8, 9, 10, 10, 13, 16$,因为有6个数据点,中位数为 $\frac{10 + 10}{2} = 10$,中位数未改变。
3. 众数:
出现次数最多的数仍然是 $10$,因此众数未改变。
【答案】:
平均数发生了改变,改变后的平均数是 $11$ 分。
中位数没有发生改变,仍然是 $10$ 分。
众数没有发生改变,仍然是 $10$ 分。
查看更多完整答案,请扫码查看


