第66页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
4. 如图,指出这些图形分别是怎样的对称图形.
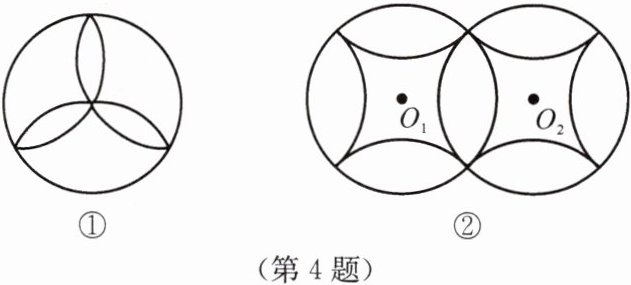

答案:
解:①和②都是轴对称图形
5. 用等分圆周的方法画如图所示的图案.
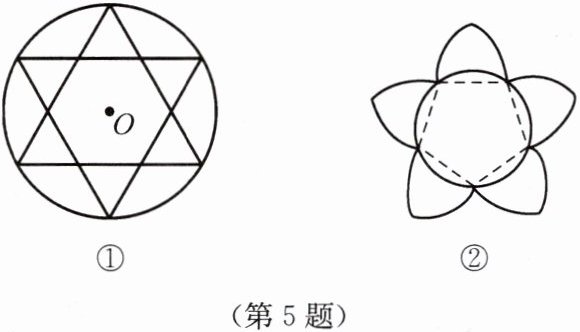

答案:
解:图①,以圆O上任一点A为圆心,圆O的半径长为半径画弧,
交圆O于B、F 两点,
再以B为圆心,圆O的半径长为半径,画弧交圆O于点C,
再以C为圆心,圆O的半径长为半径,画弧交圆O于D,
再以D为圆心,圆O的半径长为半径画弧,交圆O于E,
连接AC,AE,CE,FB,FD,BD即可得出图形
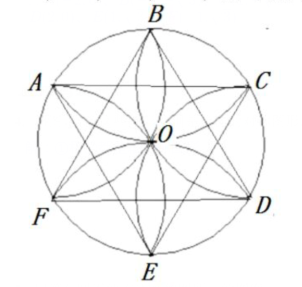
图②将圆O五等分,分别以五等分点A、B、C、D、E为圆心,
以AB长为半径画弧,即可得到图案
解:图①,以圆O上任一点A为圆心,圆O的半径长为半径画弧,
交圆O于B、F 两点,
再以B为圆心,圆O的半径长为半径,画弧交圆O于点C,
再以C为圆心,圆O的半径长为半径,画弧交圆O于D,
再以D为圆心,圆O的半径长为半径画弧,交圆O于E,
连接AC,AE,CE,FB,FD,BD即可得出图形

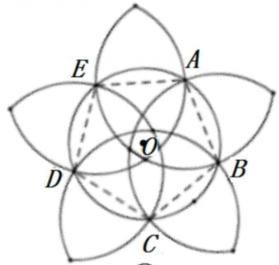
图②将圆O五等分,分别以五等分点A、B、C、D、E为圆心,
以AB长为半径画弧,即可得到图案

6. 用48m长的篱笆在空地上围成一个绿化场地,现有正三角形、正方形、正六边形、圆的四种设计方案,哪种设计方案的场地面积最大(可以利用计算器计算)?
答案:
解:正三角形边长48÷3=16(m),面积为$ \frac 12×16×8\sqrt3=64\sqrt3(m^2)$
正方形边长为: 48÷4=12(m),面积为:$ 12×12=144(m^2)$
正六边形边长为: 48÷6=8(m),面积为:$ 6×\frac 12×8×4\sqrt3=96\sqrt3(m^2) $
圆的半径为$ \frac {48}{2π}=\frac {24}{π}(m),$面积为:$ π×(\frac {24}{π})^2=\frac {576}{π}(m^2)$
∵$ 64\sqrt3<144<96\sqrt3<\frac {576}{π}$
∴圆的面积最大
正方形边长为: 48÷4=12(m),面积为:$ 12×12=144(m^2)$
正六边形边长为: 48÷6=8(m),面积为:$ 6×\frac 12×8×4\sqrt3=96\sqrt3(m^2) $
圆的半径为$ \frac {48}{2π}=\frac {24}{π}(m),$面积为:$ π×(\frac {24}{π})^2=\frac {576}{π}(m^2)$
∵$ 64\sqrt3<144<96\sqrt3<\frac {576}{π}$
∴圆的面积最大
图2-35是圆弧形铁轨的示意图,其中圆弧的半径为100 m,圆心角为90°.你能求出这段铁轨的长度吗(π取3)?
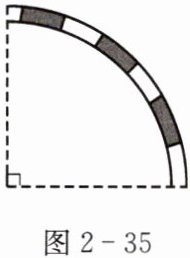

答案:
解:长度大约为$ \frac {2×3×100}4=150(\mathrm {m})$
查看更多完整答案,请扫码查看


