第85页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
6. 某商场服装部为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励.为了确定一个适当的月销售目标,商场服装部统计了每个营业员在某月的销售额(单位:万元),数据如下:
17,18,16,15,28,19,16,19,32,30,16,15,26,15,32,15,15,28,28,20.
(1)月销售额在哪个数值的人数最多?中间的月销售额是多少?平均月销售额是多少?
(2)如果想让一半左右的营业员都能达到销售目标,你认为月销售额定位多少合适?说明理由.
17,18,16,15,28,19,16,19,32,30,16,15,26,15,32,15,15,28,28,20.
(1)月销售额在哪个数值的人数最多?中间的月销售额是多少?平均月销售额是多少?
(2)如果想让一半左右的营业员都能达到销售目标,你认为月销售额定位多少合适?说明理由.
答案:
$(1)$
- **步骤一:统计各数值出现的次数
将数据整理如下:
$15$出现了$6$次;$16$出现了$3$次;$17$出现了$1$次;$18$出现了$1$次;$19$出现了$2$次;$20$出现了$1$次;$26$出现了$1$次;$28$出现了$3$次;$30$出现了$1$次;$32$出现了$2$次。
所以月销售额在$15$万元的人数最多。
步骤二:求中间的月销售额(中位数)
将数据从小到大排列:$15,15,15,15,15,15,16,16,16,17,18,19,19,20,26,28,28,28,30,32,32$。
一共有$n = 20$个数据,中位数是第$\frac{n}{2}=10$个数和第$\frac{n}{2}+1 = 11$个数的平均数,即$\frac{18 + 19}{2}=18.5$(万元)。
步骤三:求平均月销售额(平均数)
根据平均数公式$\bar{x}=\frac{1}{n}\sum_{i = 1}^{n}x_{i}$,$n = 20$,$\sum_{i=1}^{20}x_{i}=15×6 + 16×3+17+18+19×2+20+26+28×3+30+32×2$
$=90+48 + 17+18+38+20+26+84+30+64$
$=435$。
则$\bar{x}=\frac{435}{20}=21.75$(万元)。
$(2)$
月销售额定位$18.5$万元合适。
理由:因为中位数是$18.5$万元,中位数可以将数据分成前半部分和后半部分,若将月销售额定位为中位数$18.5$万元,大约有一半左右的营业员能达到销售目标。
综上,$(1)$月销售额在$15$万元的人数最多;中间的月销售额是$18.5$万元;平均月销售额是$21.75$万元。$(2)$月销售额定位$18.5$万元合适,理由如上述。
- **步骤一:统计各数值出现的次数
将数据整理如下:
$15$出现了$6$次;$16$出现了$3$次;$17$出现了$1$次;$18$出现了$1$次;$19$出现了$2$次;$20$出现了$1$次;$26$出现了$1$次;$28$出现了$3$次;$30$出现了$1$次;$32$出现了$2$次。
所以月销售额在$15$万元的人数最多。
步骤二:求中间的月销售额(中位数)
将数据从小到大排列:$15,15,15,15,15,15,16,16,16,17,18,19,19,20,26,28,28,28,30,32,32$。
一共有$n = 20$个数据,中位数是第$\frac{n}{2}=10$个数和第$\frac{n}{2}+1 = 11$个数的平均数,即$\frac{18 + 19}{2}=18.5$(万元)。
步骤三:求平均月销售额(平均数)
根据平均数公式$\bar{x}=\frac{1}{n}\sum_{i = 1}^{n}x_{i}$,$n = 20$,$\sum_{i=1}^{20}x_{i}=15×6 + 16×3+17+18+19×2+20+26+28×3+30+32×2$
$=90+48 + 17+18+38+20+26+84+30+64$
$=435$。
则$\bar{x}=\frac{435}{20}=21.75$(万元)。
$(2)$
月销售额定位$18.5$万元合适。
理由:因为中位数是$18.5$万元,中位数可以将数据分成前半部分和后半部分,若将月销售额定位为中位数$18.5$万元,大约有一半左右的营业员能达到销售目标。
综上,$(1)$月销售额在$15$万元的人数最多;中间的月销售额是$18.5$万元;平均月销售额是$21.75$万元。$(2)$月销售额定位$18.5$万元合适,理由如上述。
1.(1)在某校“我的梦想”演讲比赛中,有9名学生参加决赛,他们决赛的最终成绩各不相同.学生想要知道自己能否进入前5名,不仅要了解自己的成绩,还要了解这9名学生成绩的( ).
A.众数
B.加权平均数
C.算术平均数
D.中位数
A.众数
B.加权平均数
C.算术平均数
D.中位数
答案:
【解析】:
这个问题考察的是对中位数、众数、加权平均数和算术平均数的理解。
中位数:当数据量为奇数时,中位数是排序后位于中间的数;当数据量为偶数时,中位数是排序后中间两个数的平均值。在这个问题中,有9名学生,所以中位数就是排序后位于中间的数,即第5名的成绩。
众数:一组数据中出现次数最多的数。这个问题中,并没有提到成绩的出现次数,所以众数不适用于判断是否能进入前5名。
加权平均数和算术平均数:都是反映数据平均水平的量,但在这个问题中,我们需要知道的是自己成绩在所有成绩中的相对位置,而不是平均水平。
因此,为了知道自己是否能进入前5名,学生需要知道自己的成绩以及这9名学生成绩的中位数。如果学生的成绩大于或等于中位数,那么他就能进入前5名。
【答案】:
D. 中位数。
这个问题考察的是对中位数、众数、加权平均数和算术平均数的理解。
中位数:当数据量为奇数时,中位数是排序后位于中间的数;当数据量为偶数时,中位数是排序后中间两个数的平均值。在这个问题中,有9名学生,所以中位数就是排序后位于中间的数,即第5名的成绩。
众数:一组数据中出现次数最多的数。这个问题中,并没有提到成绩的出现次数,所以众数不适用于判断是否能进入前5名。
加权平均数和算术平均数:都是反映数据平均水平的量,但在这个问题中,我们需要知道的是自己成绩在所有成绩中的相对位置,而不是平均水平。
因此,为了知道自己是否能进入前5名,学生需要知道自己的成绩以及这9名学生成绩的中位数。如果学生的成绩大于或等于中位数,那么他就能进入前5名。
【答案】:
D. 中位数。
(2)为筹备班级的毕业联欢会,班长对全班学生爱吃哪几种水果做调查,决定最终买何种水果.下列调查数据中,最值得关注的是( ).
A.众数
B.加权平均数
C.算术平均数
D.中位数
A.众数
B.加权平均数
C.算术平均数
D.中位数
答案:
【解析】:
这个问题考查的是对统计量的理解,特别是在实际应用中应该选择哪个统计量来描述数据的“集中趋势”。在这个场景中,班长需要决定买哪种水果,这应该基于大多数学生的喜好。因此,最值得关注的应该是出现次数最多的水果,即众数。
(A)众数:一组数据中出现次数最多的数值。在这个场景下,众数代表了最受学生欢迎的水果,是决定买哪种水果的关键指标。
(B)加权平均数:考虑了每个数据点的重要性(权重)后的平均数。在这个问题中,每种水果的“重要性”并没有给出,因此加权平均数不适用。
(C)算术平均数:所有数据之和除以数据的数量。它反映了数据的“平均水平”,但不一定能反映大多数人的选择。
(D)中位数:将数据从小到大排序后,位于中间的数值。它反映了数据的“中间水平”,但同样不一定能反映大多数人的选择。
综上所述,为了决定买哪种水果,最应该关注的是众数,因为它代表了最受学生欢迎的水果。
【答案】:
A
这个问题考查的是对统计量的理解,特别是在实际应用中应该选择哪个统计量来描述数据的“集中趋势”。在这个场景中,班长需要决定买哪种水果,这应该基于大多数学生的喜好。因此,最值得关注的应该是出现次数最多的水果,即众数。
(A)众数:一组数据中出现次数最多的数值。在这个场景下,众数代表了最受学生欢迎的水果,是决定买哪种水果的关键指标。
(B)加权平均数:考虑了每个数据点的重要性(权重)后的平均数。在这个问题中,每种水果的“重要性”并没有给出,因此加权平均数不适用。
(C)算术平均数:所有数据之和除以数据的数量。它反映了数据的“平均水平”,但不一定能反映大多数人的选择。
(D)中位数:将数据从小到大排序后,位于中间的数值。它反映了数据的“中间水平”,但同样不一定能反映大多数人的选择。
综上所述,为了决定买哪种水果,最应该关注的是众数,因为它代表了最受学生欢迎的水果。
【答案】:
A
(3)某篮球队队员共有16人,每人投篮6次,下表为投进球数的次数分配表.已知该队投进球数的中位数是2.5,则众数为______.


答案:
2
2. 九年级教室里,3名同学正在为谁的实验操作成绩最好而争论,他们的5次实验操作成绩分别是:
小华:62,94,95,98,98;
小明:62,62,98,99,100;
小丽:40,62,85,99,99.
他们都认为自己的成绩最好,你的意见呢?为什么?
小华:62,94,95,98,98;
小明:62,62,98,99,100;
小丽:40,62,85,99,99.
他们都认为自己的成绩最好,你的意见呢?为什么?
答案:
解:小华成绩:平均数为(62+94+95+98+98)÷5=89.4,中位数为95,众数为98;
小明成绩:平均数为(62+62+98+99+100)÷5=84.2,中位数为98,众数为62;
小丽成绩:平均数为(40+62+85+99+99)÷5=77,中位数为85,众数为99。
若以平均数看,小华最好;以中位数看,小明最好;以众数看,小丽和小华并列最好。需根据评价标准确定,综合来看小华成绩较好,因其平均数最高且众数较高。
小明成绩:平均数为(62+62+98+99+100)÷5=84.2,中位数为98,众数为62;
小丽成绩:平均数为(40+62+85+99+99)÷5=77,中位数为85,众数为99。
若以平均数看,小华最好;以中位数看,小明最好;以众数看,小丽和小华并列最好。需根据评价标准确定,综合来看小华成绩较好,因其平均数最高且众数较高。
3. 某校元旦文艺演出中,10位评委给某个节目打分如下(单位:分):
7.20,7.25,7.00,7.10,9.50,7.30,7.20,7.20,6.10,7.25.
结合近期所学习的内容,哪一个统计量可以更好地表示上述节目得分的集中趋势?请说明理由.
7.20,7.25,7.00,7.10,9.50,7.30,7.20,7.20,6.10,7.25.
结合近期所学习的内容,哪一个统计量可以更好地表示上述节目得分的集中趋势?请说明理由.
答案:
【解析】:
本题考查了统计量的选择,用于描述数据集中程度的统计量主要有平均数、中位数和众数。我们需要根据给定数据的特性,选择合适的统计量来表示数据的集中趋势。平均数受极端值影响较大,可能不能真实反映数据的集中情况;中位数则能较好地反映数据的中心位置,但不受数据中极端值的影响;众数是出现次数最多的数,可以反映数据的普遍情况。在本题中,由于存在一个明显的极端值9.50,使用平均数来表示集中趋势可能不合适。因此,我们应该考虑使用中位数或众数。接下来,我们将数据从小到大排序,并找出中位数和众数。
【答案】:
解:
首先,将给定的数据从小到大排序:
6.10,7.00,7.10,7.20,7.20,7.20,7.25,7.25,7.30,9.50。
中位数是数据中间的数,如果数据量为奇数,则中位数是中间那个数;如果数据量为偶数,则中位数是中间两个数的平均值。在本题中,数据量为10(偶数),所以中位数是第5个数7.20和第6个数7.20的平均值,即7.20。
众数是出现次数最多的数。在本题中,7.20出现了3次,是出现次数最多的数,所以众数是7.20。
由于存在极端值9.50,使用平均数来表示集中趋势可能会受到较大影响。而中位数和众数都能较好地反映数据的集中情况。但考虑到中位数是数据中间的数,不受极端值影响,且在此数据集中,中位数和众数相同,都是7.20,所以我们可以选择中位数来表示上述节目得分的集中趋势。
因此,可以更好地表示上述节目得分的集中趋势的统计量是中位数,其值为7.20分。
本题考查了统计量的选择,用于描述数据集中程度的统计量主要有平均数、中位数和众数。我们需要根据给定数据的特性,选择合适的统计量来表示数据的集中趋势。平均数受极端值影响较大,可能不能真实反映数据的集中情况;中位数则能较好地反映数据的中心位置,但不受数据中极端值的影响;众数是出现次数最多的数,可以反映数据的普遍情况。在本题中,由于存在一个明显的极端值9.50,使用平均数来表示集中趋势可能不合适。因此,我们应该考虑使用中位数或众数。接下来,我们将数据从小到大排序,并找出中位数和众数。
【答案】:
解:
首先,将给定的数据从小到大排序:
6.10,7.00,7.10,7.20,7.20,7.20,7.25,7.25,7.30,9.50。
中位数是数据中间的数,如果数据量为奇数,则中位数是中间那个数;如果数据量为偶数,则中位数是中间两个数的平均值。在本题中,数据量为10(偶数),所以中位数是第5个数7.20和第6个数7.20的平均值,即7.20。
众数是出现次数最多的数。在本题中,7.20出现了3次,是出现次数最多的数,所以众数是7.20。
由于存在极端值9.50,使用平均数来表示集中趋势可能会受到较大影响。而中位数和众数都能较好地反映数据的集中情况。但考虑到中位数是数据中间的数,不受极端值影响,且在此数据集中,中位数和众数相同,都是7.20,所以我们可以选择中位数来表示上述节目得分的集中趋势。
因此,可以更好地表示上述节目得分的集中趋势的统计量是中位数,其值为7.20分。
4. 小亮和小莹自制了一个靶子进行投镖比赛,两人各投了10次,如图是他们投镖成绩的统计图.
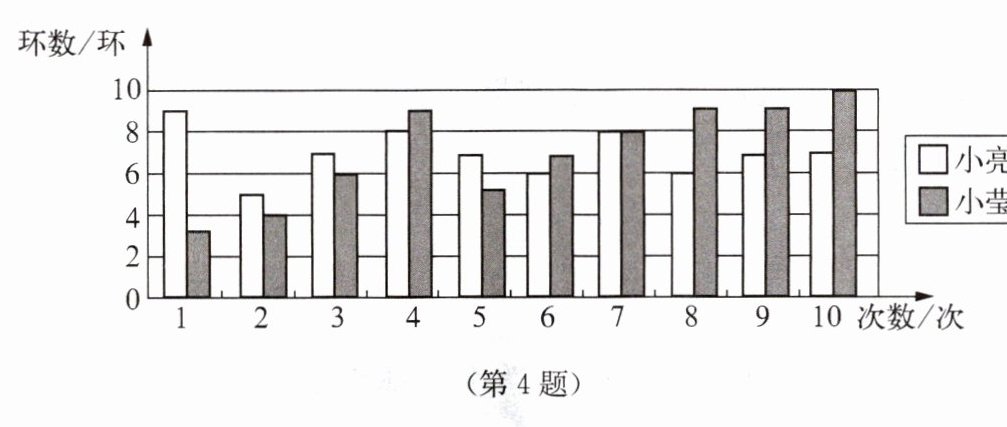
(1)根据图中信息填写下表:

(2)请从两个不同的角度评价小亮和小莹的投镖成绩.

(1)根据图中信息填写下表:

(2)请从两个不同的角度评价小亮和小莹的投镖成绩.
答案:
1. (1)
小亮:
平均数$\bar{x}_{亮}=\frac{1}{10}(3 + 4+5 + 6+7 + 7+8 + 8+9 + 10)$
先计算分子:$3 + 4+5 + 6+7 + 7+8 + 8+9 + 10=(3 + 10)+(4 + 9)+(5 + 8)+(6 + 8)+(7 + 7)=13×5 = 65$。
所以$\bar{x}_{亮}=\frac{65}{10}=6.5$。
中位数:将数据从小到大排列为$3,4,5,6,7,7,8,8,9,10$,中间两个数是$7$和$7$,则中位数$m_{亮}=\frac{7 + 7}{2}=7$。
方差$s_{亮}^{2}=\frac{1}{10}[(3 - 6.5)^{2}+(4 - 6.5)^{2}+(5 - 6.5)^{2}+(6 - 6.5)^{2}+(7 - 6.5)^{2}+(7 - 6.5)^{2}+(8 - 6.5)^{2}+(8 - 6.5)^{2}+(9 - 6.5)^{2}+(10 - 6.5)^{2}]$
$=\frac{1}{10}[(-3.5)^{2}+(-2.5)^{2}+(-1.5)^{2}+(-0.5)^{2}+0.5^{2}+0.5^{2}+1.5^{2}+1.5^{2}+2.5^{2}+3.5^{2}]$
$=\frac{1}{10}(12.25 + 6.25+2.25 + 0.25+0.25 + 0.25+2.25 + 2.25+6.25 + 12.25)$
$=\frac{1}{10}×42 = 4.2$。
小莹:
平均数$\bar{x}_{莹}=\frac{1}{10}(4 + 4+5 + 5+6 + 6+7 + 7+8 + 8)$
先计算分子:$(4 + 8)+(4 + 8)+(5 + 7)+(5 + 7)+(6 + 6)=12×5 = 60$,所以$\bar{x}_{莹}=\frac{60}{10}=6$。
中位数:将数据从小到大排列为$4,4,5,5,6,6,7,7,8,8$,中间两个数是$6$和$6$,则中位数$m_{莹}=\frac{6 + 6}{2}=6$。
方差$s_{莹}^{2}=\frac{1}{10}[(4 - 6)^{2}+(4 - 6)^{2}+(5 - 6)^{2}+(5 - 6)^{2}+(6 - 6)^{2}+(6 - 6)^{2}+(7 - 6)^{2}+(7 - 6)^{2}+(8 - 6)^{2}+(8 - 6)^{2}]$
$=\frac{1}{10}[(-2)^{2}+(-2)^{2}+(-1)^{2}+(-1)^{2}+0^{2}+0^{2}+1^{2}+1^{2}+2^{2}+2^{2}]$
$=\frac{1}{10}(4 + 4+1 + 1+0 + 0+1 + 1+4 + 4)$
$=\frac{1}{10}×18 = 1.8$。
填表如下:
|姓名|平均数|中位数|方差|
|----|----|----|----|
|小亮|$6.5$|$7$|$4.2$|
|小莹|$6$|$6$|$1.8$|
2. (2)
角度一(从平均数和中位数看):
小亮的平均数$\bar{x}_{亮}=6.5$,中位数$m_{亮}=7$;小莹的平均数$\bar{x}_{莹}=6$,中位数$m_{莹}=6$。因为$\bar{x}_{亮}>\bar{x}_{莹}$,$m_{亮}>m_{莹}$,所以从平均数和中位数来看,小亮的成绩总体上比小莹好。
角度二(从方差看):
小亮的方差$s_{亮}^{2}=4.2$,小莹的方差$s_{莹}^{2}=1.8$,因为$s_{亮}^{2}>s_{莹}^{2}$,方差越小,成绩越稳定,所以小莹的成绩比小亮稳定。
综上,(1)表格已填好;(2)从平均数和中位数看小亮成绩总体好,从方差看小莹成绩稳定。
小亮:
平均数$\bar{x}_{亮}=\frac{1}{10}(3 + 4+5 + 6+7 + 7+8 + 8+9 + 10)$
先计算分子:$3 + 4+5 + 6+7 + 7+8 + 8+9 + 10=(3 + 10)+(4 + 9)+(5 + 8)+(6 + 8)+(7 + 7)=13×5 = 65$。
所以$\bar{x}_{亮}=\frac{65}{10}=6.5$。
中位数:将数据从小到大排列为$3,4,5,6,7,7,8,8,9,10$,中间两个数是$7$和$7$,则中位数$m_{亮}=\frac{7 + 7}{2}=7$。
方差$s_{亮}^{2}=\frac{1}{10}[(3 - 6.5)^{2}+(4 - 6.5)^{2}+(5 - 6.5)^{2}+(6 - 6.5)^{2}+(7 - 6.5)^{2}+(7 - 6.5)^{2}+(8 - 6.5)^{2}+(8 - 6.5)^{2}+(9 - 6.5)^{2}+(10 - 6.5)^{2}]$
$=\frac{1}{10}[(-3.5)^{2}+(-2.5)^{2}+(-1.5)^{2}+(-0.5)^{2}+0.5^{2}+0.5^{2}+1.5^{2}+1.5^{2}+2.5^{2}+3.5^{2}]$
$=\frac{1}{10}(12.25 + 6.25+2.25 + 0.25+0.25 + 0.25+2.25 + 2.25+6.25 + 12.25)$
$=\frac{1}{10}×42 = 4.2$。
小莹:
平均数$\bar{x}_{莹}=\frac{1}{10}(4 + 4+5 + 5+6 + 6+7 + 7+8 + 8)$
先计算分子:$(4 + 8)+(4 + 8)+(5 + 7)+(5 + 7)+(6 + 6)=12×5 = 60$,所以$\bar{x}_{莹}=\frac{60}{10}=6$。
中位数:将数据从小到大排列为$4,4,5,5,6,6,7,7,8,8$,中间两个数是$6$和$6$,则中位数$m_{莹}=\frac{6 + 6}{2}=6$。
方差$s_{莹}^{2}=\frac{1}{10}[(4 - 6)^{2}+(4 - 6)^{2}+(5 - 6)^{2}+(5 - 6)^{2}+(6 - 6)^{2}+(6 - 6)^{2}+(7 - 6)^{2}+(7 - 6)^{2}+(8 - 6)^{2}+(8 - 6)^{2}]$
$=\frac{1}{10}[(-2)^{2}+(-2)^{2}+(-1)^{2}+(-1)^{2}+0^{2}+0^{2}+1^{2}+1^{2}+2^{2}+2^{2}]$
$=\frac{1}{10}(4 + 4+1 + 1+0 + 0+1 + 1+4 + 4)$
$=\frac{1}{10}×18 = 1.8$。
填表如下:
|姓名|平均数|中位数|方差|
|----|----|----|----|
|小亮|$6.5$|$7$|$4.2$|
|小莹|$6$|$6$|$1.8$|
2. (2)
角度一(从平均数和中位数看):
小亮的平均数$\bar{x}_{亮}=6.5$,中位数$m_{亮}=7$;小莹的平均数$\bar{x}_{莹}=6$,中位数$m_{莹}=6$。因为$\bar{x}_{亮}>\bar{x}_{莹}$,$m_{亮}>m_{莹}$,所以从平均数和中位数来看,小亮的成绩总体上比小莹好。
角度二(从方差看):
小亮的方差$s_{亮}^{2}=4.2$,小莹的方差$s_{莹}^{2}=1.8$,因为$s_{亮}^{2}>s_{莹}^{2}$,方差越小,成绩越稳定,所以小莹的成绩比小亮稳定。
综上,(1)表格已填好;(2)从平均数和中位数看小亮成绩总体好,从方差看小莹成绩稳定。
5. 为了解甲、乙两厂生产的同型号电子产品的使用寿命,质量检测部门分别抽取了两厂生产的各5件电子产品进行测试,测试的统计结果如下(单位:年):
甲厂:4,5,5,7,9;
乙厂:5,5,6,6,7.
(1)制作一幅统计图表示上述数据;
(2)根据上述数据,两厂都声称他们的电子产品在正常情况下的“平均”使用寿命是6年,请对两厂表述中的“平均”的含义进行解释.
甲厂:4,5,5,7,9;
乙厂:5,5,6,6,7.
(1)制作一幅统计图表示上述数据;
(2)根据上述数据,两厂都声称他们的电子产品在正常情况下的“平均”使用寿命是6年,请对两厂表述中的“平均”的含义进行解释.
答案:
(1)(由于文本限制,此处无法直接绘制统计图,实际作答时应绘制合适的统计图,如条形统计图,横轴表示电子产品序号,纵轴表示使用寿命,分别画出甲、乙两厂对应数据的条形)
(2)解:甲厂:$\frac{4 + 5 + 5 + 7 + 9}{5} = 6$,甲厂的“平均”指算术平均数。
乙厂数据排序为5,5,6,6,7,中位数是6,乙厂的“平均”指中位数。
(2)解:甲厂:$\frac{4 + 5 + 5 + 7 + 9}{5} = 6$,甲厂的“平均”指算术平均数。
乙厂数据排序为5,5,6,6,7,中位数是6,乙厂的“平均”指中位数。
查看更多完整答案,请扫码查看


