第92页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
5. 我们知道,方差的计算公式是:
$s^{2}= \frac {1}{n}[(x_{1}-\overline {x})^{2}+(x_{2}-\overline {x})^{2}+... +(x_{n}-\overline {x})^{2}],$
它需要计算每个数据与平均数的差,进而来展示整体数据的离散程度.
现在有这样一个式子:
$\frac {(x_{1}-\overline {x})+(x_{2}-\overline {x})+... +(x_{n}-\overline {x})}{n},$
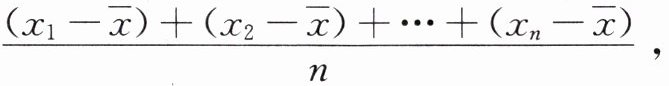
这个式子也需要计算每个数据与平均数的差,它能否用来表示数据的离散程度呢?请你判断,并说明理由.
$s^{2}= \frac {1}{n}[(x_{1}-\overline {x})^{2}+(x_{2}-\overline {x})^{2}+... +(x_{n}-\overline {x})^{2}],$
它需要计算每个数据与平均数的差,进而来展示整体数据的离散程度.
现在有这样一个式子:
$\frac {(x_{1}-\overline {x})+(x_{2}-\overline {x})+... +(x_{n}-\overline {x})}{n},$
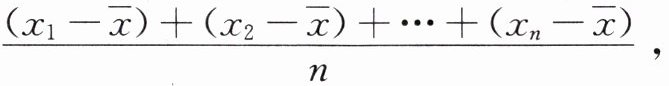
这个式子也需要计算每个数据与平均数的差,它能否用来表示数据的离散程度呢?请你判断,并说明理由.
答案:
解:这样的做法不可行
原式$=\frac {x_1+x_2+x_3+···+x_n-n\overline{x}}{n}=\overline{x}-\overline{x}=0$
故它不能反映数据的离散程度。
原式$=\frac {x_1+x_2+x_3+···+x_n-n\overline{x}}{n}=\overline{x}-\overline{x}=0$
故它不能反映数据的离散程度。
A、B两支篮球队的队员身高如下(单位:cm):
|A队|178|177|179|178|178|177|178|178|177|179|
|B队|178|177|179|176|178|180|180|178|176|178|
你能用计算器计算两支球队队员身高的平均数、方差吗?哪支球队队员的身高比较整齐?
|A队|178|177|179|178|178|177|178|178|177|179|
|B队|178|177|179|176|178|180|180|178|176|178|
你能用计算器计算两支球队队员身高的平均数、方差吗?哪支球队队员的身高比较整齐?
答案:
解:$ \overline{x_A}=(178+177+...+179)÷10=177.9(cm)$
$s^2_A=\frac 1{10}×[(178-177.9)^2+(177-177.9)^2+...+(179-177.9)^2]=0.49(cm^2)$
$\overline{x_B}=(178+177+...+178)÷10=178(cm)$
$s^2_B=\frac 1{10}×[(178-178)^2+(177-178)^2+...+(178-178)^2]=1.8(cm^2)$
∵$ s^2_B>s^2_A$
∴A队的队员身高比较整齐
$s^2_A=\frac 1{10}×[(178-177.9)^2+(177-177.9)^2+...+(179-177.9)^2]=0.49(cm^2)$
$\overline{x_B}=(178+177+...+178)÷10=178(cm)$
$s^2_B=\frac 1{10}×[(178-178)^2+(177-178)^2+...+(178-178)^2]=1.8(cm^2)$
∵$ s^2_B>s^2_A$
∴A队的队员身高比较整齐
例 为了从甲、乙两名学生中选拔一人参加科普知识竞赛,赛前对他们进行了5次培训,5次培训测试的成绩如图3-3所示.
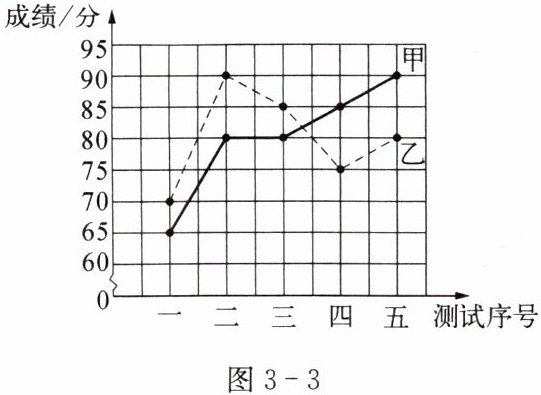
(1)分别求甲、乙两名学生5次测试成绩的平均数、方差和极差.
(2)如果你是辅导老师,会选择哪一名学生参加这次科普知识竞赛?请说明理由.
解 (1)$\overline{x}_{甲}= 80$,$\overline{x}_{乙}= 80$,$s^{2}_{甲}= 70$,$s^{2}_{乙}= 50$,甲的极差= 25,乙的极差= 20;
(2)选择乙学生参加科普知识竞赛,因为$s^{2}_{甲}>s^{2}_{乙}$,甲的极差>乙的极差,而$\overline{x}_{甲}= \overline{x}_{乙}$,乙学生的成绩相对稳定.
说明 计算平均数、方差时,若数据较多又复杂,可利用计算器计算.

(1)分别求甲、乙两名学生5次测试成绩的平均数、方差和极差.
(2)如果你是辅导老师,会选择哪一名学生参加这次科普知识竞赛?请说明理由.
解 (1)$\overline{x}_{甲}= 80$,$\overline{x}_{乙}= 80$,$s^{2}_{甲}= 70$,$s^{2}_{乙}= 50$,甲的极差= 25,乙的极差= 20;
(2)选择乙学生参加科普知识竞赛,因为$s^{2}_{甲}>s^{2}_{乙}$,甲的极差>乙的极差,而$\overline{x}_{甲}= \overline{x}_{乙}$,乙学生的成绩相对稳定.
说明 计算平均数、方差时,若数据较多又复杂,可利用计算器计算.
答案:
解:
(1)由图可知,甲五次测试成绩为:65,80,80,85,90;乙五次测试成绩为:70,90,85,75,80。
$\overline{x}_{甲}=\frac{65+80+80+85+90}{5}=80$
$s^{2}_{甲}=\frac{1}{5}[(65-80)^{2}+(80-80)^{2}+(80-80)^{2}+(85-80)^{2}+(90-80)^{2}]=70$
甲的极差$=90-65=25$
$\overline{x}_{乙}=\frac{70+90+85+75+80}{5}=80$
$s^{2}_{乙}=\frac{1}{5}[(70-80)^{2}+(90-80)^{2}+(85-80)^{2}+(75-80)^{2}+(80-80)^{2}]=50$
乙的极差$=90-70=20$
(2)选择乙学生参加科普知识竞赛,因为$\overline{x}_{甲}=\overline{x}_{乙}$,$s^{2}_{甲}>s^{2}_{乙}$,甲的极差>乙的极差,乙学生的成绩相对稳定。
(1)由图可知,甲五次测试成绩为:65,80,80,85,90;乙五次测试成绩为:70,90,85,75,80。
$\overline{x}_{甲}=\frac{65+80+80+85+90}{5}=80$
$s^{2}_{甲}=\frac{1}{5}[(65-80)^{2}+(80-80)^{2}+(80-80)^{2}+(85-80)^{2}+(90-80)^{2}]=70$
甲的极差$=90-65=25$
$\overline{x}_{乙}=\frac{70+90+85+75+80}{5}=80$
$s^{2}_{乙}=\frac{1}{5}[(70-80)^{2}+(90-80)^{2}+(85-80)^{2}+(75-80)^{2}+(80-80)^{2}]=50$
乙的极差$=90-70=20$
(2)选择乙学生参加科普知识竞赛,因为$\overline{x}_{甲}=\overline{x}_{乙}$,$s^{2}_{甲}>s^{2}_{乙}$,甲的极差>乙的极差,乙学生的成绩相对稳定。
查看更多完整答案,请扫码查看


