第27页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
例1 一本书的封面长为27 cm,宽为21 cm,正中央是一个与整个封面长、宽比例相同的矩形.要使四周的彩色边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,如何设计四周边衬的宽度(精确到0.1 cm)?
分析 封面的长与宽之比为27:21=9:7,中央矩形的长与宽之比也应是9:7,由此判断上、下边衬与左、右边衬的宽度之比也是9:7.
解 设上、下边衬的宽均为9x cm,左、右边衬的宽均为7x cm,则中央矩形的长为(27-18x)cm,宽为(21-14x)cm.
根据题意,得
(27-18x)(21-14x)=$\frac{3}{4}×27×21$.
整理,得
$16x^{2}-48x+9=0$.
解这个方程,得
$x_{1}=\frac{6-3\sqrt{3}}{4}$,$x_{2}=\frac{6+3\sqrt{3}}{4}$(不合题意,舍去).
9x=9×$\frac{6-3\sqrt{3}}{4}$≈1.8,7x=7×$\frac{6-3\sqrt{3}}{4}$≈1.4.
答 上、下边衬的宽均为1.8 cm,左、右边衬的宽均为1.4 cm.
分析 封面的长与宽之比为27:21=9:7,中央矩形的长与宽之比也应是9:7,由此判断上、下边衬与左、右边衬的宽度之比也是9:7.
解 设上、下边衬的宽均为9x cm,左、右边衬的宽均为7x cm,则中央矩形的长为(27-18x)cm,宽为(21-14x)cm.
根据题意,得
(27-18x)(21-14x)=$\frac{3}{4}×27×21$.
整理,得
$16x^{2}-48x+9=0$.
解这个方程,得
$x_{1}=\frac{6-3\sqrt{3}}{4}$,$x_{2}=\frac{6+3\sqrt{3}}{4}$(不合题意,舍去).
9x=9×$\frac{6-3\sqrt{3}}{4}$≈1.8,7x=7×$\frac{6-3\sqrt{3}}{4}$≈1.4.
答 上、下边衬的宽均为1.8 cm,左、右边衬的宽均为1.4 cm.
答案:
【解析】:
本题主要考察一元二次方程的建立与求解。
首先,根据题意,封面的长与宽之比为$27:21=9:7$,因此中央矩形的长与宽之比也应是$9:7$。
设上、下边衬的宽均为$9x$ cm,左、右边衬的宽均为$7x$ cm。
然后,可以表示出中央矩形的长和宽,分别为$(27-18x)$ cm 和 $(21-14x)$ cm。
接着,根据题目条件“四周的彩色边衬所占面积是封面面积的四分之一”,可以列出等式:
$(27-18x)(21-14x) = \frac{3}{4} × 27 × 21$,
整理这个等式,得到一个一元二次方程:
$16x^2 - 48x + 9 = 0$,
解这个方程,得到两个解,其中一个解不符合实际情况(边衬宽度不能为负或过大),所以被舍去。
最后,根据符合实际情况的解,计算出上、下边衬和左、右边衬的宽度。
【答案】:
解:设上、下边衬的宽均为$9x$ cm,左、右边衬的宽均为$7x$ cm。
则中央矩形的长为$(27-18x)$ cm,宽为$(21-14x)$ cm。
根据题意,列出等式:
$(27-18x)(21-14x) = \frac{3}{4} × 27 × 21$,
整理得到一元二次方程:
$16x^2 - 48x + 9 = 0$,
解方程得到:
$x_1 = \frac{6-3\sqrt{3}}{4}$,
$x_2 = \frac{6+3\sqrt{3}}{4}$(不合题意,舍去),
计算边衬宽度:
上、下边衬的宽均为$9 × \frac{6-3\sqrt{3}}{4} \approx 1.8$ (cm),
左、右边衬的宽均为$7 × \frac{6-3\sqrt{3}}{4} \approx 1.4$ (cm),
答:上、下边衬的宽均为$1.8$ cm,左、右边衬的宽均为$1.4$ cm。
本题主要考察一元二次方程的建立与求解。
首先,根据题意,封面的长与宽之比为$27:21=9:7$,因此中央矩形的长与宽之比也应是$9:7$。
设上、下边衬的宽均为$9x$ cm,左、右边衬的宽均为$7x$ cm。
然后,可以表示出中央矩形的长和宽,分别为$(27-18x)$ cm 和 $(21-14x)$ cm。
接着,根据题目条件“四周的彩色边衬所占面积是封面面积的四分之一”,可以列出等式:
$(27-18x)(21-14x) = \frac{3}{4} × 27 × 21$,
整理这个等式,得到一个一元二次方程:
$16x^2 - 48x + 9 = 0$,
解这个方程,得到两个解,其中一个解不符合实际情况(边衬宽度不能为负或过大),所以被舍去。
最后,根据符合实际情况的解,计算出上、下边衬和左、右边衬的宽度。
【答案】:
解:设上、下边衬的宽均为$9x$ cm,左、右边衬的宽均为$7x$ cm。
则中央矩形的长为$(27-18x)$ cm,宽为$(21-14x)$ cm。
根据题意,列出等式:
$(27-18x)(21-14x) = \frac{3}{4} × 27 × 21$,
整理得到一元二次方程:
$16x^2 - 48x + 9 = 0$,
解方程得到:
$x_1 = \frac{6-3\sqrt{3}}{4}$,
$x_2 = \frac{6+3\sqrt{3}}{4}$(不合题意,舍去),
计算边衬宽度:
上、下边衬的宽均为$9 × \frac{6-3\sqrt{3}}{4} \approx 1.8$ (cm),
左、右边衬的宽均为$7 × \frac{6-3\sqrt{3}}{4} \approx 1.4$ (cm),
答:上、下边衬的宽均为$1.8$ cm,左、右边衬的宽均为$1.4$ cm。
例2 某企业生产一种新型太阳能热水器,前年获利1000万元,今年获利1560万元,今年的利润增长率比去年的利润增长率多10%.去年和今年的利润增长率各是多少?
分析 利用等量关系:增长利润=利润基数×利润增长率,设去年的利润增长率为x,那么有下表:
|时间|利润基数/万元|利润增长率|利润/万元|
|----|----|----|----|
|去年|1000|x|1000(1+x)|
|今年|1000(1+x)|x+0.1|1000(1+x)(1+x+0.1)|
根据今年获利1560万元,可以列出方程.
解 设去年的利润增长率是x,则今年的利润增长率是x+0.1.
根据题意,得
1000(1+x)(1+x+0.1)=1560.
整理,得
$x^{2}+2.1x-0.46=0$.
解这个方程,得
$x_{1}=0.2$,$x_{2}=-2.3$(不合题意,舍去).
x+0.1=0.2+0.1=0.3.
答 去年的利润增长率是20%,今年的利润增长率是30%.
分析 利用等量关系:增长利润=利润基数×利润增长率,设去年的利润增长率为x,那么有下表:
|时间|利润基数/万元|利润增长率|利润/万元|
|----|----|----|----|
|去年|1000|x|1000(1+x)|
|今年|1000(1+x)|x+0.1|1000(1+x)(1+x+0.1)|
根据今年获利1560万元,可以列出方程.
解 设去年的利润增长率是x,则今年的利润增长率是x+0.1.
根据题意,得
1000(1+x)(1+x+0.1)=1560.
整理,得
$x^{2}+2.1x-0.46=0$.
解这个方程,得
$x_{1}=0.2$,$x_{2}=-2.3$(不合题意,舍去).
x+0.1=0.2+0.1=0.3.
答 去年的利润增长率是20%,今年的利润增长率是30%.
答案:
解:设去年的利润增长率是$x$,则今年的利润增长率是$x + 0.1$。
根据题意,得$1000(1 + x)(1 + x + 0.1) = 1560$。
整理,得$x^2 + 2.1x - 0.46 = 0$。
解这个方程,得$x_1 = 0.2$,$x_2 = -2.3$(不合题意,舍去)。
$x + 0.1 = 0.2 + 0.1 = 0.3$。
答:去年的利润增长率是$20\%$,今年的利润增长率是$30\%$。
根据题意,得$1000(1 + x)(1 + x + 0.1) = 1560$。
整理,得$x^2 + 2.1x - 0.46 = 0$。
解这个方程,得$x_1 = 0.2$,$x_2 = -2.3$(不合题意,舍去)。
$x + 0.1 = 0.2 + 0.1 = 0.3$。
答:去年的利润增长率是$20\%$,今年的利润增长率是$30\%$。
1. 一个人的血压与其年龄及性别有关.对女性来说,正常的收缩压p(mmHg)与年龄x(岁)大致满足关系:$p=0.01x^{2}+0.05x+107$;对男性来说,正常的收缩压p(mmHg)与年龄x(岁)大致满足关系:$p=0.006x^{2}-0.02x+120$.
(1)已知一名女性的收缩压为120 mmHg,那么她的年龄大概是多少?
(2)已知一名男性的收缩压为130 mmHg,那么他的年龄大概是多少?
(1)已知一名女性的收缩压为120 mmHg,那么她的年龄大概是多少?
(2)已知一名男性的收缩压为130 mmHg,那么他的年龄大概是多少?
答案:
【解析】:
本题主要考察的是一元二次方程的求解。
对于女性,有公式 $p = 0.01x^2 + 0.05x + 107$。
将 $p = 120$ 代入公式,得到方程 $0.01x^2 + 0.05x + 107 = 120$。
化简后得到一元二次方程 $0.01x^2 + 0.05x - 13 = 0$。
使用求根公式求解此方程,得到两个解,选择符合实际情况的解。
对于男性,有公式 $p = 0.006x^2 - 0.02x + 120$。
将 $p = 130$ 代入公式,得到方程 $0.006x^2 - 0.02x + 120 = 130$。
化简后得到一元二次方程 $0.006x^2 - 0.02x - 10 = 0$。
同样使用求根公式求解此方程,并选择符合实际情况的解。
【答案】:
(1)解:
将$p = 120$代入$p = 0.01x^2 + 0.05x + 107$,
得$0.01x^2 + 0.05x + 107 = 120$,
化简得$0.01x^2 + 0.05x - 13 = 0$,
通过求根公式$x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$,
其中$a = 0.01$,$b = 0.05$,$c = -13$,
解得$x_{1} = \frac{-0.05 + \sqrt{0.05^2 - 4 × 0.01 × (-13)}}{2 × 0.01} \approx 34$,
$x_{2} = \frac{-0.05 - \sqrt{0.05^2 - 4 × 0.01 × (-13)}}{2 × 0.01} \approx -39$(舍去),
所以,这名女性的年龄大概是34岁。
(2)解:
将$p = 130$代入$p = 0.006x^2 - 0.02x + 120$,
得$0.006x^2 - 0.02x + 120 = 130$,
化简得$0.006x^2 - 0.02x - 10 = 0$,
通过求根公式,其中$a = 0.006$,$b = -0.02$,$c = -10$,
解得$x_{1} = \frac{0.02 + \sqrt{(-0.02)^2 - 4 × 0.006 × (-10)}}{2 × 0.006} \approx 43$,
$x_{2} = \frac{0.02 - \sqrt{(-0.02)^2 - 4 × 0.006 × (-10)}}{2 × 0.006} \approx -38$(舍去),
所以,这名男性的年龄大概是43岁。
本题主要考察的是一元二次方程的求解。
对于女性,有公式 $p = 0.01x^2 + 0.05x + 107$。
将 $p = 120$ 代入公式,得到方程 $0.01x^2 + 0.05x + 107 = 120$。
化简后得到一元二次方程 $0.01x^2 + 0.05x - 13 = 0$。
使用求根公式求解此方程,得到两个解,选择符合实际情况的解。
对于男性,有公式 $p = 0.006x^2 - 0.02x + 120$。
将 $p = 130$ 代入公式,得到方程 $0.006x^2 - 0.02x + 120 = 130$。
化简后得到一元二次方程 $0.006x^2 - 0.02x - 10 = 0$。
同样使用求根公式求解此方程,并选择符合实际情况的解。
【答案】:
(1)解:
将$p = 120$代入$p = 0.01x^2 + 0.05x + 107$,
得$0.01x^2 + 0.05x + 107 = 120$,
化简得$0.01x^2 + 0.05x - 13 = 0$,
通过求根公式$x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$,
其中$a = 0.01$,$b = 0.05$,$c = -13$,
解得$x_{1} = \frac{-0.05 + \sqrt{0.05^2 - 4 × 0.01 × (-13)}}{2 × 0.01} \approx 34$,
$x_{2} = \frac{-0.05 - \sqrt{0.05^2 - 4 × 0.01 × (-13)}}{2 × 0.01} \approx -39$(舍去),
所以,这名女性的年龄大概是34岁。
(2)解:
将$p = 130$代入$p = 0.006x^2 - 0.02x + 120$,
得$0.006x^2 - 0.02x + 120 = 130$,
化简得$0.006x^2 - 0.02x - 10 = 0$,
通过求根公式,其中$a = 0.006$,$b = -0.02$,$c = -10$,
解得$x_{1} = \frac{0.02 + \sqrt{(-0.02)^2 - 4 × 0.006 × (-10)}}{2 × 0.006} \approx 43$,
$x_{2} = \frac{0.02 - \sqrt{(-0.02)^2 - 4 × 0.006 × (-10)}}{2 × 0.006} \approx -38$(舍去),
所以,这名男性的年龄大概是43岁。
2. 李先生存入银行1万元,先存一年定期,一年后将本息自动转存为另一个一年定期.假设一年定期存款的年利率不变,已知两年后共得本息1.06万元,那么存款的年利率为多少?
答案:
【解析】:
本题主要考察的是一元二次方程的应用,特别是关于复利计算的问题。
首先,设存款的年利率为$x$(以小数形式表示,例如:年利率为$3\%$,则$x=0.03$)。
李先生最初存入1万元,一年后他的本息和为$1 × (1+x)$万元。
两年后,他的本息和将变为$1 × (1+x) × (1+x) = 1 × (1+x)^{2}$万元。
根据题目,这个数等于1.06万元。
因此,可以建立方程:
$(1+x)^{2} = 1.06$,
展开方程,得到:
$1 + 2x + x^{2} = 1.06$,
整理方程,得到一元二次方程:
$x^{2} + 2x - 0.06 = 0$,
解这个方程,我们可以使用求根公式:
$x = \frac{-b \pm \sqrt{b^{2} - 4ac}}{2a}$,
其中,$a = 1, b = 2, c = -0.06$。
代入求根公式,解得:
$x_{1} = \frac{-2 + \sqrt{2^{2} - 4 × 1 × (-0.06)}}{2 × 1} \approx 0.0298$(取正值,因为利率不能为负),
$x_{2} = \frac{-2 - \sqrt{2^{2} - 4 × 1 × (-0.06)}}{2 × 1}$(舍去,因为利率不能为负),
将$x_{1}$转换为百分比形式,即$x_{1} \approx 3\%$。
【答案】:
存款的年利率为$3\%$。
本题主要考察的是一元二次方程的应用,特别是关于复利计算的问题。
首先,设存款的年利率为$x$(以小数形式表示,例如:年利率为$3\%$,则$x=0.03$)。
李先生最初存入1万元,一年后他的本息和为$1 × (1+x)$万元。
两年后,他的本息和将变为$1 × (1+x) × (1+x) = 1 × (1+x)^{2}$万元。
根据题目,这个数等于1.06万元。
因此,可以建立方程:
$(1+x)^{2} = 1.06$,
展开方程,得到:
$1 + 2x + x^{2} = 1.06$,
整理方程,得到一元二次方程:
$x^{2} + 2x - 0.06 = 0$,
解这个方程,我们可以使用求根公式:
$x = \frac{-b \pm \sqrt{b^{2} - 4ac}}{2a}$,
其中,$a = 1, b = 2, c = -0.06$。
代入求根公式,解得:
$x_{1} = \frac{-2 + \sqrt{2^{2} - 4 × 1 × (-0.06)}}{2 × 1} \approx 0.0298$(取正值,因为利率不能为负),
$x_{2} = \frac{-2 - \sqrt{2^{2} - 4 × 1 × (-0.06)}}{2 × 1}$(舍去,因为利率不能为负),
将$x_{1}$转换为百分比形式,即$x_{1} \approx 3\%$。
【答案】:
存款的年利率为$3\%$。
3. 某果园今年栽种果树200棵,现计划扩大栽种数量,使今后两年的栽种数量都比前一年增长一个相同的百分数,这样三年(包括今年)的栽种数量为1400棵.求这个百分数.
答案:
【解析】:
本题主要考查一元二次方程的应用。
设这个百分数为$x$,则第一年栽种数量为$200(1+x)$棵,第二年栽种数量为$200(1+x)^{2}$棵。
根据题意,三年(包括今年)的栽种数量为1400棵,因此我们可以列出方程:
$200 + 200(1+x) + 200(1+x)^{2} = 1400$
展开方程得:
$200 + 200 + 200x + 200 + 400x + 200x^{2} = 1400$
$200x^{2} + 600x - 800 = 0$
$x^{2} + 3x - 4 = 0$
通过求解这个一元二次方程,我们可以找到$x$的值。
【答案】:
解:
设这个百分数为$x$,根据题意我们可以列出方程:
$200 + 200(1+x) + 200(1+x)^{2} = 1400$
展开并整理得:
$200x^{2} + 600x - 800 = 0$
$x^{2} + 3x - 4 = 0$
通过因式分解或者使用求根公式,我们可以得到:
$x_{1} = 1$,$x_{2} = -4$
由于百分数不能为负,所以$x_{2} = -4$不符合题意,舍去。
因此,这个百分数为$100\%$(因为$x=1$,即增长$100\%$)。
本题主要考查一元二次方程的应用。
设这个百分数为$x$,则第一年栽种数量为$200(1+x)$棵,第二年栽种数量为$200(1+x)^{2}$棵。
根据题意,三年(包括今年)的栽种数量为1400棵,因此我们可以列出方程:
$200 + 200(1+x) + 200(1+x)^{2} = 1400$
展开方程得:
$200 + 200 + 200x + 200 + 400x + 200x^{2} = 1400$
$200x^{2} + 600x - 800 = 0$
$x^{2} + 3x - 4 = 0$
通过求解这个一元二次方程,我们可以找到$x$的值。
【答案】:
解:
设这个百分数为$x$,根据题意我们可以列出方程:
$200 + 200(1+x) + 200(1+x)^{2} = 1400$
展开并整理得:
$200x^{2} + 600x - 800 = 0$
$x^{2} + 3x - 4 = 0$
通过因式分解或者使用求根公式,我们可以得到:
$x_{1} = 1$,$x_{2} = -4$
由于百分数不能为负,所以$x_{2} = -4$不符合题意,舍去。
因此,这个百分数为$100\%$(因为$x=1$,即增长$100\%$)。
4. 有五个连续整数,前三个数的平方和等于后两个数的平方和.求这五个数.
答案:
解:设这五个连续整数的中间数为$x$,则这五个数分别为$x - 2$,$x - 1$,$x$,$x + 1$,$x + 2$。
根据题意,得$(x - 2)^2 + (x - 1)^2 + x^2 = (x + 1)^2 + (x + 2)^2$。
展开,得$x^2 - 4x + 4 + x^2 - 2x + 1 + x^2 = x^2 + 2x + 1 + x^2 + 4x + 4$。
合并同类项,得$3x^2 - 6x + 5 = 2x^2 + 6x + 5$。
移项、合并同类项,得$x^2 - 12x = 0$。
因式分解,得$x(x - 12) = 0$。
解得$x_1 = 0$,$x_2 = 12$。
当$x = 0$时,这五个数为$-2$,$-1$,$0$,$1$,$2$;
当$x = 12$时,这五个数为$10$,$11$,$12$,$13$,$14$。
答:这五个数为$-2$,$-1$,$0$,$1$,$2$或$10$,$11$,$12$,$13$,$14$。
根据题意,得$(x - 2)^2 + (x - 1)^2 + x^2 = (x + 1)^2 + (x + 2)^2$。
展开,得$x^2 - 4x + 4 + x^2 - 2x + 1 + x^2 = x^2 + 2x + 1 + x^2 + 4x + 4$。
合并同类项,得$3x^2 - 6x + 5 = 2x^2 + 6x + 5$。
移项、合并同类项,得$x^2 - 12x = 0$。
因式分解,得$x(x - 12) = 0$。
解得$x_1 = 0$,$x_2 = 12$。
当$x = 0$时,这五个数为$-2$,$-1$,$0$,$1$,$2$;
当$x = 12$时,这五个数为$10$,$11$,$12$,$13$,$14$。
答:这五个数为$-2$,$-1$,$0$,$1$,$2$或$10$,$11$,$12$,$13$,$14$。
5. 如图,在Rt△ACB中,∠C=90°,点P、Q同时由A、B两点出发,分别沿AC、BC方向向点C匀速移动,它们的速度都是1 m/s.多少时间后△PCQ的面积是Rt△ACB面积的一半?
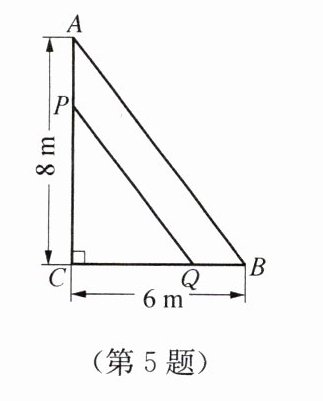

答案:
$解:设经过x秒后△PCQ的面积为△ACB面积的一半$
$\frac {(8-x)(6-x)}2=12$
$解得x_1=2,x_2=12(舍去)$
$答:经过2秒后△PCQ的面积为△ACB面积的一半。$
$\frac {(8-x)(6-x)}2=12$
$解得x_1=2,x_2=12(舍去)$
$答:经过2秒后△PCQ的面积为△ACB面积的一半。$
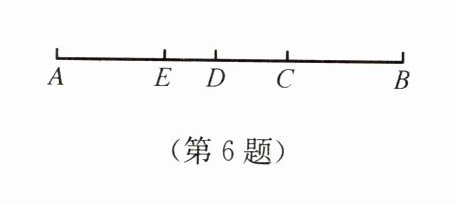
*6. 如图,线段AB的长为1.
(1)若线段AB上的点C满足表达式$AC^{2}=BC\cdot AB$,求线段AC的长度;
(2)若线段AC上的点D满足表达式$AD^{2}=CD\cdot AC$,求线段AD的长度;
(3)若线段AD上的点E满足表达式$AE^{2}=DE\cdot AD$,求线段AE的长度.
上面各小题的结果反映了什么规律?
(1)若线段AB上的点C满足表达式$AC^{2}=BC\cdot AB$,求线段AC的长度;
(2)若线段AC上的点D满足表达式$AD^{2}=CD\cdot AC$,求线段AD的长度;
(3)若线段AD上的点E满足表达式$AE^{2}=DE\cdot AD$,求线段AE的长度.
上面各小题的结果反映了什么规律?

答案:
【解析】:
本题主要考察一元二次方程的求解以及黄金分割点的性质。
(1) 设线段AC的长度为$x$,则线段BC的长度为$1 - x$。
根据题意,有$AC^{2} = BC \cdot AB$,代入已知条件$AB = 1$,得到方程:
$x^{2} = (1 - x) × 1$,
$x^{2} + x - 1 = 0$,
解这个一元二次方程,得到两个解,其中一个解大于1(由于线段长度不能为负或大于整段长度,所以此解舍去),另一个解为线段AC的长度:
$x = \frac{\sqrt{5} - 1}{2}$(负值已舍去),
所以,线段AC的长度为$\frac{\sqrt{5} - 1}{2}$。
(2) 设线段AD的长度为$y$,则线段CD的长度为$x - y=\frac{\sqrt{5} - 1}{2}-y$。
根据题意,有$AD^{2} = CD \cdot AC$,代入$AC = \frac{\sqrt{5} - 1}{2}$,得到方程:
$y^{2} = (\frac{\sqrt{5} - 1}{2} - y) × \frac{\sqrt{5} - 1}{2}$,
$y^{2}+\frac{\sqrt{5} - 1}{2}y- \frac{\sqrt{5} - 1}{2}×\frac{\sqrt{5} - 1}{2}=0$,
解这个一元二次方程,得到两个解,其中一个解大于$\frac{\sqrt{5} - 1}{2}$(由于线段长度不能为负或大于整段长度,所以此解舍去),另一个解为线段AD的长度:
$y = \frac{3 - \sqrt{5}}{2}$(负值及大于$\frac{\sqrt{5} - 1}{2}$的值已舍去),
所以,线段AD的长度为$\frac{3 - \sqrt{5}}{2}$。
(3) 设线段AE的长度为$z$,则线段DE的长度为$y - z=\frac{3 - \sqrt{5}}{2}-z$。
根据题意,有$AE^{2} = DE \cdot AD$,代入$AD = \frac{3 - \sqrt{5}}{2}$,得到方程:
$z^{2} = (\frac{3 - \sqrt{5}}{2} - z) × \frac{3 - \sqrt{5}}{2}$,
$z^{2}+\frac{3 - \sqrt{5}}{2}z- \frac{3 - \sqrt{5}}{2}×\frac{3 - \sqrt{5}}{2}=0$,
解这个一元二次方程,得到两个解,其中一个解大于$\frac{3 - \sqrt{5}}{2}$(由于线段长度不能为负或大于整段长度,所以此解舍去),另一个解为线段AE的长度:
$z = \frac{\sqrt{5} - 1}{2} × \frac{3 - \sqrt{5}}{2} = \sqrt{5} - 2$(负值及大于$\frac{3 - \sqrt{5}}{2}$的值已舍去),
所以,线段AE的长度为$\sqrt{5} - 2$。
上面各小题的结果反映了黄金分割点性质的传递性,即若点C是线段AB的黄金分割点,则点D也是线段AC的黄金分割点,点E也是线段AD的黄金分割点。
【答案】:
(1)线段AC的长度为$\frac{\sqrt{5} - 1}{2}$;
(2)线段AD的长度为$\frac{3 - \sqrt{5}}{2}$;
(3)线段AE的长度为$\sqrt{5} - 2$;
规律:上面各小题的结果反映了黄金分割点性质的传递性。
本题主要考察一元二次方程的求解以及黄金分割点的性质。
(1) 设线段AC的长度为$x$,则线段BC的长度为$1 - x$。
根据题意,有$AC^{2} = BC \cdot AB$,代入已知条件$AB = 1$,得到方程:
$x^{2} = (1 - x) × 1$,
$x^{2} + x - 1 = 0$,
解这个一元二次方程,得到两个解,其中一个解大于1(由于线段长度不能为负或大于整段长度,所以此解舍去),另一个解为线段AC的长度:
$x = \frac{\sqrt{5} - 1}{2}$(负值已舍去),
所以,线段AC的长度为$\frac{\sqrt{5} - 1}{2}$。
(2) 设线段AD的长度为$y$,则线段CD的长度为$x - y=\frac{\sqrt{5} - 1}{2}-y$。
根据题意,有$AD^{2} = CD \cdot AC$,代入$AC = \frac{\sqrt{5} - 1}{2}$,得到方程:
$y^{2} = (\frac{\sqrt{5} - 1}{2} - y) × \frac{\sqrt{5} - 1}{2}$,
$y^{2}+\frac{\sqrt{5} - 1}{2}y- \frac{\sqrt{5} - 1}{2}×\frac{\sqrt{5} - 1}{2}=0$,
解这个一元二次方程,得到两个解,其中一个解大于$\frac{\sqrt{5} - 1}{2}$(由于线段长度不能为负或大于整段长度,所以此解舍去),另一个解为线段AD的长度:
$y = \frac{3 - \sqrt{5}}{2}$(负值及大于$\frac{\sqrt{5} - 1}{2}$的值已舍去),
所以,线段AD的长度为$\frac{3 - \sqrt{5}}{2}$。
(3) 设线段AE的长度为$z$,则线段DE的长度为$y - z=\frac{3 - \sqrt{5}}{2}-z$。
根据题意,有$AE^{2} = DE \cdot AD$,代入$AD = \frac{3 - \sqrt{5}}{2}$,得到方程:
$z^{2} = (\frac{3 - \sqrt{5}}{2} - z) × \frac{3 - \sqrt{5}}{2}$,
$z^{2}+\frac{3 - \sqrt{5}}{2}z- \frac{3 - \sqrt{5}}{2}×\frac{3 - \sqrt{5}}{2}=0$,
解这个一元二次方程,得到两个解,其中一个解大于$\frac{3 - \sqrt{5}}{2}$(由于线段长度不能为负或大于整段长度,所以此解舍去),另一个解为线段AE的长度:
$z = \frac{\sqrt{5} - 1}{2} × \frac{3 - \sqrt{5}}{2} = \sqrt{5} - 2$(负值及大于$\frac{3 - \sqrt{5}}{2}$的值已舍去),
所以,线段AE的长度为$\sqrt{5} - 2$。
上面各小题的结果反映了黄金分割点性质的传递性,即若点C是线段AB的黄金分割点,则点D也是线段AC的黄金分割点,点E也是线段AD的黄金分割点。
【答案】:
(1)线段AC的长度为$\frac{\sqrt{5} - 1}{2}$;
(2)线段AD的长度为$\frac{3 - \sqrt{5}}{2}$;
(3)线段AE的长度为$\sqrt{5} - 2$;
规律:上面各小题的结果反映了黄金分割点性质的传递性。
查看更多完整答案,请扫码查看


