《2025年学习与评价江苏教育出版社九年级数学上册苏科版》

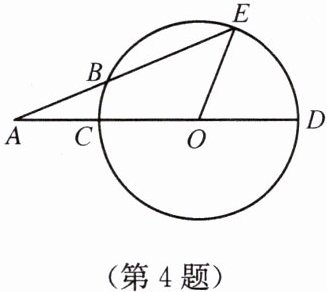
4. 如图,CD为⊙O的直径,∠EOD= 69°,AE交⊙O于点B,且AB= OC. 求∠A的度数.

答案： 解：连接OB
∵OB =OC =OE
∴∠E=∠OBE
∵AB = OC
∴AB =OB
∴∠A=∠AOB
∴∠OBE=∠A+∠AOB =2∠A
∴∠E=∠OBE=2∠A
∵∠A+∠E=∠EOD =69°
∴∠A+2∠A =69°
∴∠A = 23°

5. 如图,⊙O的半径OA、OB分别交弦CD于点E、F,且CE= DF.
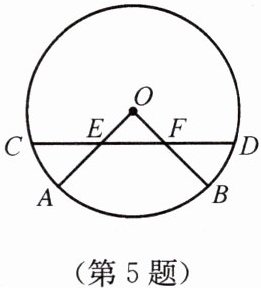
求证：△OEF是等腰三角形.

答案：
证明：过点O作OG⊥CD于点G ，则CG= DG
∵CE=DF
∴CG-CE=DG-DF ，即EG= FG
在△OEG 与△OFG 中，
$\begin{cases}OG=OG\\∠OGE=∠OGF\\EG= FG\end{cases}$
∴$△OEG≌△OFG(\mathrm {SAS})$
∴OE=OF ，即△OEF是等腰三角形

6. 已知⊙O的直径AB= 10,点C在⊙O上,且CD⊥AB,垂足为D,CD= 4. 请画出相应的图形,并求AD和DB的长.

答案：
解：符合情况的有两种情况，如图所示

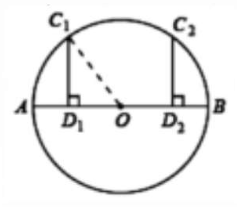
∵AB=10
∴AO=OB=5
∵CD=4，
∴$ OD=\sqrt{5^{2}-4^{2}}= 3$
当D点在A、O之间时， AD=AO-OD=5-3= 2；DB=DO+OB=3+5=8
当D点在B、O之间时， AD= AO+OD=5+3=8；DB=OB-OD=5-3=2
即AD与DB的长分别为2 ， 8或8，2

将一张正三角形纸片绕其中心O旋转多少度,能与它本身完全重合？
将一张正方形纸片绕其中心O旋转多少度,能与它本身完全重合？
将一张圆形纸片绕其圆心O旋转多少度,能与它本身完全重合？由此你发现了什么？

答案： 解：能与自身重合的最小角度：正三角形旋转120°，正方形旋转90°，圆旋转任意角度都能重合
发现旋转的最小角度为$ \frac {360°}n$

例1 如图2-4,在⊙O中,$\widehat{AB}= \widehat{AC}$,$\angle ACB= 60^\circ$.
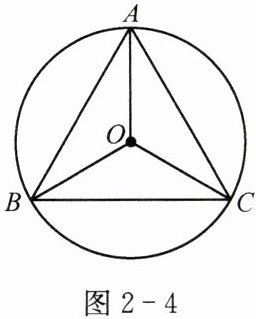
求证：$\angle AOB= \angle BOC= \angle AOC$.
证明 $\because \widehat{AB}= \widehat{AC}$,
$\therefore AB= AC$,$\triangle ABC$是等腰三角形.
又$\because \angle ACB= 60^\circ$,
$\therefore \triangle ABC$是等边三角形,$AB= BC= CA$.
$\therefore \angle AOB= \angle BOC= \angle AOC$.

答案： 【解析】：本题考查圆的对称性和等边三角形的判定与性质，利用了圆的弦相等则所对的弧相等以及等边三角形的三个内角都是$60^\circ$的性质。
已知$\widehat{AB} = \widehat{AC}$，根据在同圆或等圆中，相等的弧所对的弦相等，可得$AB = AC$，所以$\triangle ABC$是等腰三角形。
又因为$\angle ACB = 60^{\circ}$，且等腰三角形中有一个角是$60^{\circ}$时，这个三角形是等边三角形，所以$\triangle ABC$是等边三角形，那么$AB = BC = CA$。
根据在同圆或等圆中，相等的弦所对的圆心角相等，因为$AB = BC = CA$，所以$\angle AOB = \angle BOC = \angle AOC$。
【答案】：证明：$\because \widehat{AB} = \widehat{AC}$，
$\therefore AB = AC$，$\triangle ABC$是等腰三角形。
又$\because \angle ACB = 60^{\circ}$，
$\therefore \triangle ABC$是等边三角形，
$\therefore AB = BC = CA$。
$\therefore \angle AOB = \angle BOC = \angle AOC$。