第68页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
2. 选择题:
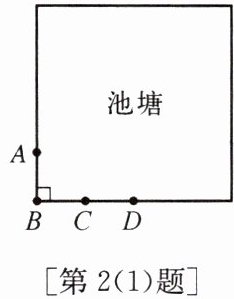
(1) 如图,边长为12 m的正方形池塘的周围是草地,池塘边A、B、C、D处各有一棵树,且AB= BC= CD= 3 m.现用长4 m的绳子将一只羊拴在其中的一棵树上,为了使羊在草地上活动区域的面积最大,应将绳子拴在(
A. A处
B. B处
C. C处
D. D处
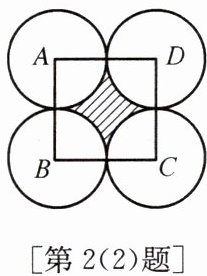
(2) 如图是半径为1的四个等圆,图中阴影部分的面积为(
A. $ 2(4-\pi) $
B. $ 8-\pi $
C. $ 4-2\pi $
D. $ 4-\pi $
(1) 如图,边长为12 m的正方形池塘的周围是草地,池塘边A、B、C、D处各有一棵树,且AB= BC= CD= 3 m.现用长4 m的绳子将一只羊拴在其中的一棵树上,为了使羊在草地上活动区域的面积最大,应将绳子拴在(
B
).A. A处
B. B处
C. C处


D. D处
(2) 如图是半径为1的四个等圆,图中阴影部分的面积为(
D
).A. $ 2(4-\pi) $
B. $ 8-\pi $
C. $ 4-2\pi $
D. $ 4-\pi $
答案:
B
D
D
3. 已知扇形的圆心角为150°,弧长为20π cm,求扇形的半径.
答案:
解:设扇形的半径为r
$ 2πr×\frac {150}{360}=20π$
r=24
答:扇形的半径为24厘米。
$ 2πr×\frac {150}{360}=20π$
r=24
答:扇形的半径为24厘米。
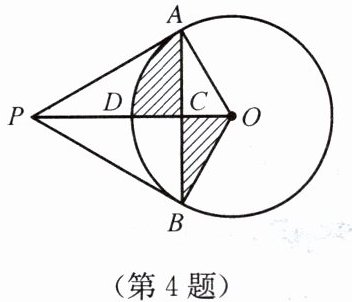
4. 如图,PA、PB是半径为1的⊙O的两条切线,切点分别为A、B,$ \angle APB= 60^{\circ} $,OP与弦AB交于点C,与⊙O交于点D.求阴影部分的面积(结果保留π).

答案:
解:
∵PA, PB为圆O的两条切线
∴PA=PB,∠PAO=∠PBO=90°
∵OA=OB
∴△PAO≌△PBO (SAS)
∴∠APO =∠BPO,∠AOP=∠BOP
∵∠APB=60°
∴$∠APO=\frac 12∠APB= 30°$
∴∠AOP=90°-30°= 60°
∵OA= OB ,∠AOC=∠BOC,OC= OC,
∴△AOC≌△BOC(SAS)
∴S_{△AOC} = S_{△BOC}
∴$S_{阴影}=S_{扇形OAD}=\frac {60π}{360}=\frac {π}6$
故阴影部分的面积为$\frac {π}6$
∵PA, PB为圆O的两条切线
∴PA=PB,∠PAO=∠PBO=90°
∵OA=OB
∴△PAO≌△PBO (SAS)
∴∠APO =∠BPO,∠AOP=∠BOP
∵∠APB=60°
∴$∠APO=\frac 12∠APB= 30°$
∴∠AOP=90°-30°= 60°
∵OA= OB ,∠AOC=∠BOC,OC= OC,
∴△AOC≌△BOC(SAS)
∴S_{△AOC} = S_{△BOC}
∴$S_{阴影}=S_{扇形OAD}=\frac {60π}{360}=\frac {π}6$
故阴影部分的面积为$\frac {π}6$
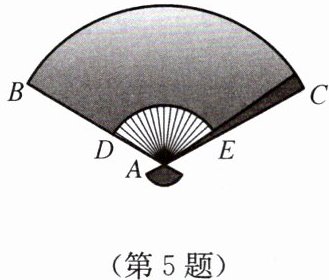
5. 如图,一把折扇完全打开后,外侧两竹条AB和AC的夹角为120°,AD长为5 cm,AB长为15 cm.求折扇单面贴纸部分的面积(结果保留π).

答案:
解:由题意得,面积为$ \frac {120°×π×15^{2}}{360°}-\frac {120°×π×5^{2}}{360°}=\frac {200}3π(\ \mathrm {cm^2})$
查看更多完整答案,请扫码查看


