第69页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
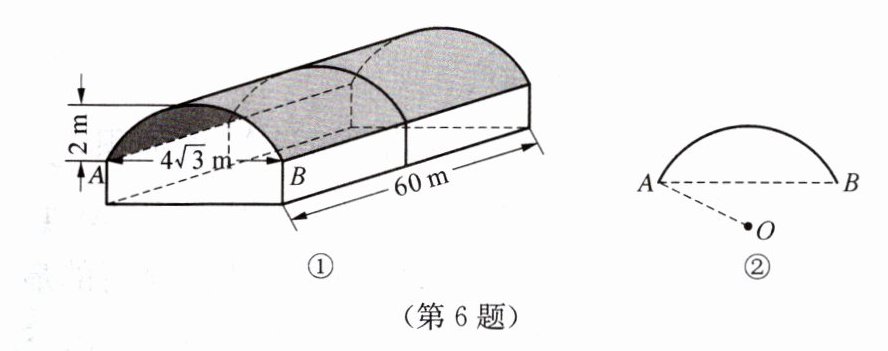
*6. 图①是某学校存放学生自行车的车棚示意图(尺寸如图标注),车棚顶部是圆柱侧面的一部分,其展开图是矩形.图②是车棚顶部横截面的示意图,$ \overset{\frown}{AB} $所在圆的圆心为O.车棚顶部是用帆布覆盖的,求覆盖棚顶的帆布的面积(不考虑接缝等因素,计算结果保留π).

答案:
解:连接OB ,过点O作OE⊥AB ,垂足为E,交AB于F,如图
由垂径定理,可知:E是AB中点,F是$\widehat{AB}$中点
∴EF是弓形高,
∴$ AE=\frac 12AB= 2\sqrt3,$ EF= 2
设半径为R米,则OE=(R-2)米
在Rt△AOE中,由勾股定理,得
$R^2=(R-2)^2+ (2\sqrt3 )^2$
解得R=4
∴$OE=\frac 12OA$
∴∠OAB=30°
∴∠AOE=60°
∴∠AOB =120°
∴$\widehat{AB}=\frac {120×4π}{180}=\frac 83π($米)
面积为$\frac 83π×60=160π($平方米)
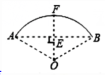
解:连接OB ,过点O作OE⊥AB ,垂足为E,交AB于F,如图
由垂径定理,可知:E是AB中点,F是$\widehat{AB}$中点
∴EF是弓形高,
∴$ AE=\frac 12AB= 2\sqrt3,$ EF= 2
设半径为R米,则OE=(R-2)米
在Rt△AOE中,由勾股定理,得
$R^2=(R-2)^2+ (2\sqrt3 )^2$
解得R=4
∴$OE=\frac 12OA$
∴∠OAB=30°
∴∠AOE=60°
∴∠AOB =120°
∴$\widehat{AB}=\frac {120×4π}{180}=\frac 83π($米)
面积为$\frac 83π×60=160π($平方米)

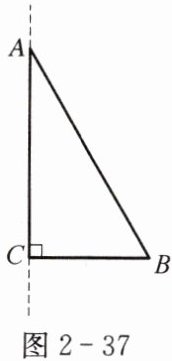
如图2-37,把Rt△ABC沿着直角边AC旋转1周,得到什么样的几何体? 在这个几何体中,AC、BC、AB分别叫什么?

答案:
解:得到一个圆锥
AC为圆锥的高,BC为圆锥底面半径,AB为圆锥的母线
AC为圆锥的高,BC为圆锥底面半径,AB为圆锥的母线
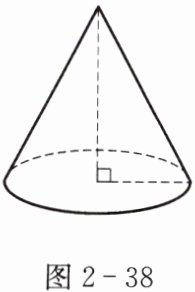
例1 如图2-38,圆锥的底面半径是6,母线的长是13.求圆锥的侧面积.
分析 圆锥的侧面展开图是一个扇形.由于已知圆锥的底面半径和母线的长,所以直接利用公式$S= \pi rl$求得.
解 圆锥的侧面积$S_{侧}= \pi rl$
$=\pi×6×13$
$=78\pi$.
分析 圆锥的侧面展开图是一个扇形.由于已知圆锥的底面半径和母线的长,所以直接利用公式$S= \pi rl$求得.
解 圆锥的侧面积$S_{侧}= \pi rl$
$=\pi×6×13$
$=78\pi$.

答案:
【解析】:本题考查圆锥侧面积的计算。圆锥的侧面积公式为$S = \pi rl$,其中$r$是底面半径,$l$是母线长。题目中已给出圆锥底面半径$r = 6$,母线长$l = 13$,将其代入公式即可求出圆锥的侧面积。
【答案】:解:已知圆锥底面半径$r = 6$,母线长$l = 13$。
根据圆锥侧面积公式$S_{侧}=\pi rl$,可得:
$S_{侧}=\pi×6×13 = 78\pi$。
所以,圆锥的侧面积是$78\pi$。
【答案】:解:已知圆锥底面半径$r = 6$,母线长$l = 13$。
根据圆锥侧面积公式$S_{侧}=\pi rl$,可得:
$S_{侧}=\pi×6×13 = 78\pi$。
所以,圆锥的侧面积是$78\pi$。
例2 如图2-39,一个圆锥的底面半径是10 cm,母线长是40 cm.
(1)求它的侧面展开图的圆心角和侧面积.
(2)有一只小虫从点A出发沿着圆锥侧面绕一圈爬行到母线SA的中点B,它爬行的最短路程是多少?
分析 圆锥的侧面展开图是一个扇形,其半径为圆锥的母线,弧长为圆锥底面圆的周长.根据“两点之间,线段最短”的性质得到线段AB的长是小虫爬行的最短路程.
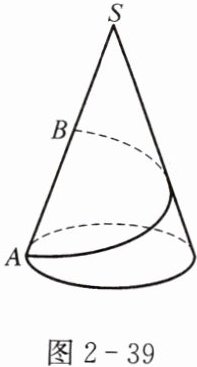
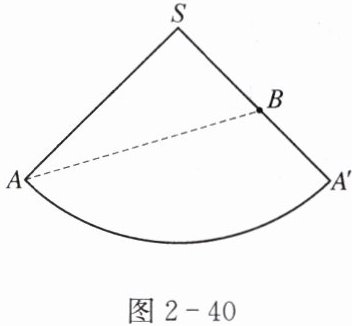
解 如图2-40,将圆锥沿着母线SA剪开,展放在平面上,得到扇形SAA'.
(1)设该圆锥的平面展开图的圆心角$\angle ASA'= n^{\circ}$.
∵圆锥底面圆的周长等于$\overset{\frown}{AA'}$的长,
∴$\frac{n\pi×40}{180}= 2\pi×10$,解得$n= 90$.
∴$\angle ASA'= 90^{\circ}$.
∵圆锥的侧面积就是扇形SAA'的面积,
∴圆锥的侧面积为:$\pi×10×40= 400\pi(cm^{2})$.
(2)连接AB,线段AB的长为小虫爬行的最短路程.
在Rt△ASB中,$\angle ASB= 90^{\circ}$,$SA= 40$,$SB= 20$,
∴$AB= \sqrt{40^{2}+20^{2}}= 20\sqrt{5}(cm)$.
∴小虫从点A爬行到点B的最短路程是$20\sqrt{5}cm$.
(1)求它的侧面展开图的圆心角和侧面积.
(2)有一只小虫从点A出发沿着圆锥侧面绕一圈爬行到母线SA的中点B,它爬行的最短路程是多少?
分析 圆锥的侧面展开图是一个扇形,其半径为圆锥的母线,弧长为圆锥底面圆的周长.根据“两点之间,线段最短”的性质得到线段AB的长是小虫爬行的最短路程.

解 如图2-40,将圆锥沿着母线SA剪开,展放在平面上,得到扇形SAA'.
(1)设该圆锥的平面展开图的圆心角$\angle ASA'= n^{\circ}$.
∵圆锥底面圆的周长等于$\overset{\frown}{AA'}$的长,
∴$\frac{n\pi×40}{180}= 2\pi×10$,解得$n= 90$.
∴$\angle ASA'= 90^{\circ}$.
∵圆锥的侧面积就是扇形SAA'的面积,
∴圆锥的侧面积为:$\pi×10×40= 400\pi(cm^{2})$.
(2)连接AB,线段AB的长为小虫爬行的最短路程.
在Rt△ASB中,$\angle ASB= 90^{\circ}$,$SA= 40$,$SB= 20$,
∴$AB= \sqrt{40^{2}+20^{2}}= 20\sqrt{5}(cm)$.
∴小虫从点A爬行到点B的最短路程是$20\sqrt{5}cm$.

答案:
解:将圆锥沿着母线SA剪开,展放在平面上,得到扇形SAA'。
(1)设该圆锥的平面展开图的圆心角∠ASA'=n°。
∵圆锥底面圆的周长等于$\overset{\frown}{AA'}$的长,
∴$\frac{n\pi×40}{180}=2\pi×10$,解得n=90。
∴∠ASA'=90°。
圆锥的侧面积为:π×10×40=400π(cm²)。
(2)连接AB,线段AB的长为小虫爬行的最短路程。
在Rt△ASB中,∠ASB=90°,SA=40,SB=20,
∴AB=$\sqrt{40^{2}+20^{2}}=20\sqrt{5}$(cm)。
∴小虫从点A爬行到点B的最短路程是$20\sqrt{5}$cm。
(1)设该圆锥的平面展开图的圆心角∠ASA'=n°。
∵圆锥底面圆的周长等于$\overset{\frown}{AA'}$的长,
∴$\frac{n\pi×40}{180}=2\pi×10$,解得n=90。
∴∠ASA'=90°。
圆锥的侧面积为:π×10×40=400π(cm²)。
(2)连接AB,线段AB的长为小虫爬行的最短路程。
在Rt△ASB中,∠ASB=90°,SA=40,SB=20,
∴AB=$\sqrt{40^{2}+20^{2}}=20\sqrt{5}$(cm)。
∴小虫从点A爬行到点B的最短路程是$20\sqrt{5}$cm。
查看更多完整答案,请扫码查看


