第64页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
我们可以根据圆的轴对称性和旋转不变性研究圆的性质,类似地,研究正多边形的性质也可以采用相同的思路,请画几个正多边形尝试着研究.
答案:
解:由正多边形的轴对称性我们可以得到正多边形如下的性质:垂直于正多边形的一条边的
对称轴平分正多边形的边,并且平分正多边形的中心角(正多边形每一边所对的外接圆的圆心角)
正n边形都是旋转对称图形,最小的旋转角就是$ \frac {360°}n,$也就是说,正n边形旋转$ \frac {360°}n$可以与自身重合
可以发现正多边形有如下性质:正多边形的每条边相等,正多边形的每个中心角相等
对称轴平分正多边形的边,并且平分正多边形的中心角(正多边形每一边所对的外接圆的圆心角)
正n边形都是旋转对称图形,最小的旋转角就是$ \frac {360°}n,$也就是说,正n边形旋转$ \frac {360°}n$可以与自身重合
可以发现正多边形有如下性质:正多边形的每条边相等,正多边形的每个中心角相等
例 已知$\odot O$,作圆的内接正八边形.
分析 可以从两条途径考虑:一是利用量角器,只要将圆八等分即可;二是可以先用直尺和圆规作出正四边形,再利用"垂直于弦的直径平分这条弦及其所对的弧"这一性质,作垂直于四条边的直径来完成.
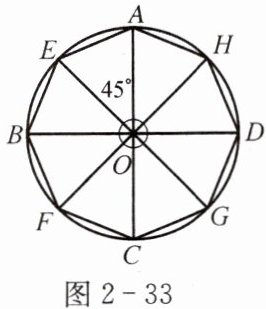
解 方法一:将圆八等分,即将圆心角$360^\circ$等分成八份,每一份为$45^\circ$,依次连接八个等分点所成的八边形就是所要求作的正八边形(图2-33).
方法二:
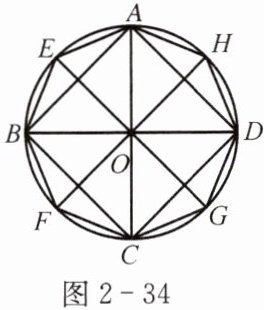
(1)先作两条互相垂直的直径AC、BD,依次连接AB、BC、CD、DA,得到正四边形ABCD;
(2)过圆心O分别作四条边的垂线交弧$\widehat{AB}$、$\widehat{BC}$、$\widehat{CD}$、$\widehat{DA}$于点E、F、G、H,依次连接AE、EB、BF、FC、CG、GD、DH、HA,所得到的八边形AEBFCGDH就是所要求作的正八边形(图2-34).
说明 (1)将圆八等分,就是将以圆心O为顶点的$360^\circ$圆心角八等分,利用量角器每隔$45^\circ$作一个等分点,这里根据"相等的圆心角所对的弧相等"以及"相等的弧所对的弦相等"的性质;(2)方法二依据"垂直于弦的直径平分弦并且平分弦所对的弧"这一性质.
分析 可以从两条途径考虑:一是利用量角器,只要将圆八等分即可;二是可以先用直尺和圆规作出正四边形,再利用"垂直于弦的直径平分这条弦及其所对的弧"这一性质,作垂直于四条边的直径来完成.
解 方法一:将圆八等分,即将圆心角$360^\circ$等分成八份,每一份为$45^\circ$,依次连接八个等分点所成的八边形就是所要求作的正八边形(图2-33).


方法二:
(1)先作两条互相垂直的直径AC、BD,依次连接AB、BC、CD、DA,得到正四边形ABCD;
(2)过圆心O分别作四条边的垂线交弧$\widehat{AB}$、$\widehat{BC}$、$\widehat{CD}$、$\widehat{DA}$于点E、F、G、H,依次连接AE、EB、BF、FC、CG、GD、DH、HA,所得到的八边形AEBFCGDH就是所要求作的正八边形(图2-34).
说明 (1)将圆八等分,就是将以圆心O为顶点的$360^\circ$圆心角八等分,利用量角器每隔$45^\circ$作一个等分点,这里根据"相等的圆心角所对的弧相等"以及"相等的弧所对的弦相等"的性质;(2)方法二依据"垂直于弦的直径平分弦并且平分弦所对的弧"这一性质.
答案:
解 方法一:将圆八等分,即将圆心角$360^{\circ}$等分成八份,每一份为$45^{\circ}$,依次连接八个等分点所成的八边形就是所要求作的正八边形。
方法二:
(1) 先作两条互相垂直的直径$AC$、$BD$,依次连接$AB$、$BC$、$CD$、$DA$,得到正四边形$ABCD$;
(2) 过圆心$O$分别作四条边的垂线交弧$\widehat{AB}$、$\widehat{BC}$、$\widehat{CD}$、$\widehat{DA}$于点$E$、$F$、$G$、$H$,依次连接$AE$、$EB$、$BF$、$FC$、$CG$、$GD$、$DH$、$HA$,所得到的八边形$AEBFCGDH$就是所要求作的正八边形。
方法二:
(1) 先作两条互相垂直的直径$AC$、$BD$,依次连接$AB$、$BC$、$CD$、$DA$,得到正四边形$ABCD$;
(2) 过圆心$O$分别作四条边的垂线交弧$\widehat{AB}$、$\widehat{BC}$、$\widehat{CD}$、$\widehat{DA}$于点$E$、$F$、$G$、$H$,依次连接$AE$、$EB$、$BF$、$FC$、$CG$、$GD$、$DH$、$HA$,所得到的八边形$AEBFCGDH$就是所要求作的正八边形。
查看更多完整答案,请扫码查看


