第73页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
1. (1)请用圆规和直尺在方框内画一个跟下面左图完全相同的风车图。

(2)补充一个条件,使得能计算出图中涂色部分的面积。
我补充的条件是
(3)写出计算涂色面积的数量关系式。
涂色部分面积=

(2)补充一个条件,使得能计算出图中涂色部分的面积。
我补充的条件是
大圆的半径为r
(3)写出计算涂色面积的数量关系式。
涂色部分面积=
$\frac{\pi}{2}r^{2}$
答案:
1.
(1)图略
(2)示例:大圆的半径为r
(3)$\frac{\pi}{2}r^{2}$
(1)图略
(2)示例:大圆的半径为r
(3)$\frac{\pi}{2}r^{2}$
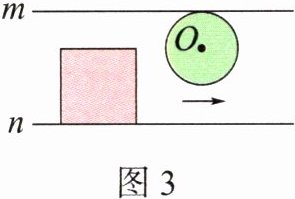
2. (新角度)如图所示,在相距12 cm的两条平行线m和n之间,有一个边长为8 cm的正方形和直径为8 cm的圆O。正方形保持不动,圆O沿直线m以每秒2 cm的速度向右平移。
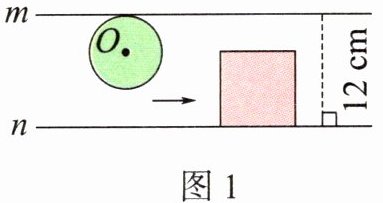
(1)在移动的过程中,圆O与正方形最大的重叠部分的面积是
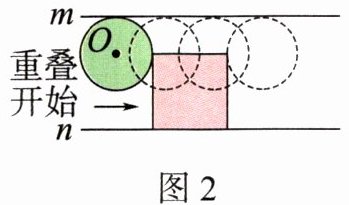
(2)如图2,圆和正方形有重叠部分的时间持续



(1)在移动的过程中,圆O与正方形最大的重叠部分的面积是
25.12
cm²。(2)如图2,圆和正方形有重叠部分的时间持续
8
秒。
答案:
2.
(1)25.12
(2)8
(1)25.12
(2)8
3. 如图,两个圆只有一个公共点C,大圆直径AC为50 cm,小圆直径BC为30 cm。甲、乙两只蚂蚁同时从C点出发,甲蚂蚁以每秒0.6 cm的速度顺时针沿着大圆圆周爬行,乙蚂蚁以同样的速度顺时针沿着小圆圆周爬行。(π取3)
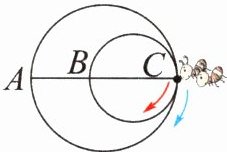
(1)乙蚂蚁第一次爬回到C点时,需要(
(2)当乙蚂蚁第一次爬回到C点时,甲蚂蚁是否已经经过了A点?
(3)甲、乙两只蚂蚁各自沿着圆周不间断地反复爬行,它们是否会在C点相遇?如果相遇,那么此时甲蚂蚁至少爬了几圈?如果不能相遇,那么请说明理由。

(1)乙蚂蚁第一次爬回到C点时,需要(
150
)秒。(2)当乙蚂蚁第一次爬回到C点时,甲蚂蚁是否已经经过了A点?
3×50÷2=75(cm) 0.6×150=90(cm) 90>75,甲蚂蚁已经经过了A点
(3)甲、乙两只蚂蚁各自沿着圆周不间断地反复爬行,它们是否会在C点相遇?如果相遇,那么此时甲蚂蚁至少爬了几圈?如果不能相遇,那么请说明理由。
会在C点相遇。甲蚂蚁第一次回到C点需要3×50÷0.6=250(秒) 150和250的最小公倍数是750 750÷250=3(圈)
答案:
3.
(1)150
(2)$3×50÷2=75(\text{cm})$ $0.6×150=90(\text{cm})$ $90>75$,甲蚂蚁已经经过了A点
(3)会在C点相遇。甲蚂蚁第一次回到C点需要$3×50÷0.6=250(\text{秒})$ 150和250的最小公倍数是750 $750÷250=3(\text{圈})$
(1)150
(2)$3×50÷2=75(\text{cm})$ $0.6×150=90(\text{cm})$ $90>75$,甲蚂蚁已经经过了A点
(3)会在C点相遇。甲蚂蚁第一次回到C点需要$3×50÷0.6=250(\text{秒})$ 150和250的最小公倍数是750 $750÷250=3(\text{圈})$
查看更多完整答案,请扫码查看


