第65页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
1. 求涂色部分的面积。
(1)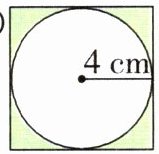
①$S_{正}$:
②$S_{圆}$:
③$S_{涂色}$:
④若圆的半径为$r\ cm$,则涂色部分的面积为(
(2)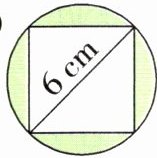
①$S_{圆}$:
②$S_{正}$:
③$S_{涂色}$:
④若圆半径为$r\ cm$,则涂色部分的面积为(
(3)如图,圆A和圆B中两个等腰直角三角形的面积都是$5\ cm^2$,圆A与圆B的面积之比是(
(1)

①$S_{正}$:
$(4×2)^{2}=64(cm^{2})$
②$S_{圆}$:
$3.14×4^{2}=50.24(cm^{2})$
③$S_{涂色}$:
$64-50.24=13.76(cm^{2})$
④若圆的半径为$r\ cm$,则涂色部分的面积为(
$0.86r^{2}$
)$cm^2$。(2)

①$S_{圆}$:
$3.14×(6÷2)^{2}=28.26(cm^{2})$
②$S_{正}$:
$6×6÷2=18(cm^{2})$
③$S_{涂色}$:
$28.26-18=10.26(cm^{2})$
④若圆半径为$r\ cm$,则涂色部分的面积为(
$1.14r^{2}$
)$cm^2$。
(3)如图,圆A和圆B中两个等腰直角三角形的面积都是$5\ cm^2$,圆A与圆B的面积之比是(
$2:1$
)。
答案:
1.
(1)①$(4×2)^{2}=64(cm^{2})$ ②$3.14×4^{2}=50.24(cm^{2})$ ③$64-50.24=13.76(cm^{2})$ ④$0.86r^{2}$
(2)①$3.14×(6÷2)^{2}=28.26(cm^{2})$ ②$6×6÷2=18(cm^{2})$ ③$28.26-18=10.26(cm^{2})$ ④$1.14r^{2}$
(3)$2:1$
(1)①$(4×2)^{2}=64(cm^{2})$ ②$3.14×4^{2}=50.24(cm^{2})$ ③$64-50.24=13.76(cm^{2})$ ④$0.86r^{2}$
(2)①$3.14×(6÷2)^{2}=28.26(cm^{2})$ ②$6×6÷2=18(cm^{2})$ ③$28.26-18=10.26(cm^{2})$ ④$1.14r^{2}$
(3)$2:1$
2.(天文景观)日环食是日食的一种天文现象,发生时太阳的中心部分黑暗,边缘仍然明亮,形成光环,某天高明上空出现了罕见的日环食。右下图是乐乐拍的一张日环食照片,他把照片放在一个边长是$2\ \text{dm}$的正方形相框中,刚好形成了我们常见的外方内圆图形,此时这个圆最大的面积是多少平方厘米?


答案:
$3.14×(2÷2)^{2}=3.14(dm^{2})$ $3.14dm^{2}=314cm^{2}$
3. 倩倩通过大量的计算发现,在正方形中画一个最大的圆,无论圆的半径怎么变化,正方形的面积与圆的面积的比始终是$4:\pi$。下图是一个边长为$4\ \text{cm}$的正方形,请在这个正方形里画出最大的圆,然后计算这个正方形面积与圆面积的比是不是$4:\pi$。
我会画: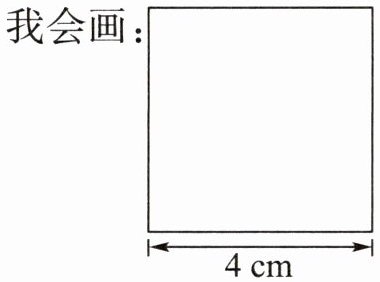
我的推导过程:______
我会画:

我的推导过程:______
答案:
图略 正方形的面积:$4×4=16(cm^{2})$ 圆的半径:$4÷2=2(cm)$ 圆的面积:$π×2^{2}=4π(cm^{2})$ 正方形的面积:圆的面积$=16:4π=4:π$
4. 如图,图中圆的周长是$12.56\ \text{cm}$,圆的面积正好等于长方形的面积。求涂色部分的面积。
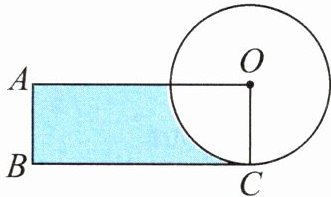

答案:
$12.56÷3.14÷2=2(cm)$ $3.14×2^{2}=12.56(cm^{2})$ $12.56-12.56×\frac {1}{4}=9.42(cm^{2})$
5. 如图,圆中的三个正方形(涂色部分)甲、乙、丙的边长分别是$3\ cm$、$2\ cm$、$1\ cm$,圆的面积是(
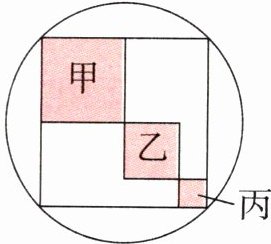
56.52
)$cm^2$。
答案:
56.52
查看更多完整答案,请扫码查看


