《2025年阳光同学课时优化作业六年级数学上册人教版》

4. 在下图中表示出$\frac{3}{4}÷3$的含义,并填一填。

方法一:$\frac{3}{4}÷3= \frac{(\quad)÷(\quad)}{4}= \frac{(\quad)}{(\quad)}$
方法二:$\frac{3}{4}÷3= \frac{3}{4}×\frac{(\quad)}{(\quad)}= \frac{(\quad)}{(\quad)}$

答案：
示例: 3　3　$\frac{1}{4}$　　$\frac{1}{3}$　$\frac{1}{4}$

5. 把$\frac{9}{10}\ \text{m}$长的绳子平均截成若干段,一共剪了5次,平均每段长多少米?

答案： 5+1=6(段)　$\frac{9}{10}$÷6=$\frac{3}{20}$(m)

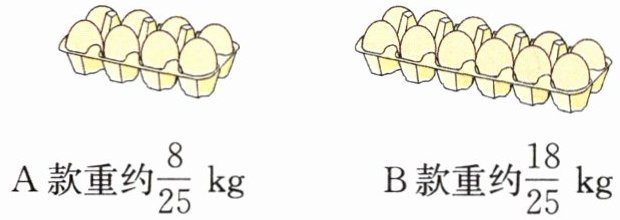
6. 妈妈想自己做一些蛋黄酥,需要5个鸡蛋,图中两款鸡蛋,选择哪款,可以放入蛋黄酥里更多的鸡蛋?

答案： A款:$\frac{8}{25}$÷8=$\frac{1}{25}$(kg)
B款:$\frac{18}{25}$÷12=$\frac{3}{50}$(kg)
　$\frac{1}{25}$＜$\frac{3}{50}$,选择B款

7. (说理表达)玲玲认为,分数除以整数可以用“分子不变,分母乘这个整数作分母”计算,如:$\frac{7}{9}÷2= \frac{7}{9×2}= \frac{7}{18}$。你认为玲玲想到的方法能否计算出所有分数除以整数的正确结果?写出你的判断理由。

答案： 玲玲想的方法能计算出所有的分数除以整数(0除外)的正确结果　因为分数除以整数，分子不变，分母乘这个整数作分母，就相当于乘这个整数的倒数，符合分数除以整数的计算法则。但是这个整数是0时，不成立，因为0不能作除数(分母)