第80页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
3. 用火车运一批煤,当装满5节车厢又20吨时,正好装了这批煤的60%。照这样计算,如果要将这批煤一次全部运走,正好装满9节车厢。这批煤共多少吨?(4分)
答案:
20÷(60% - 5/9)=450(吨)
4. 甲、乙两车分别从A、B两地同时出发,相向而行,它们的速度比是$3:2$,C地在A、B两地之间(如图),甲车行6小时到达C地,乙车行11小时到达C地。甲、乙两车出发后几小时在途中相遇?(4分)
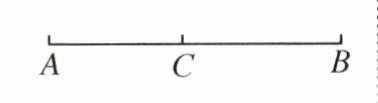
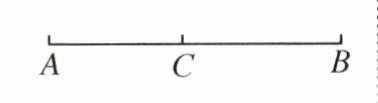
答案:
(6×3+11×2)÷(3+2)=8(小时)
5. 要把1米长的优质铜管锯成长38毫米和长90毫米两种规格的小铜管,每锯一次都要损耗1毫米铜管。现在要使所损耗的铜管最少,锯得38毫米的铜管有多少段?90毫米的铜管有多少段?(4分)
答案:
1米=1000毫米 1000+1=1001(毫米)38+1=39(毫米) 90+1=91(毫米)列表如下:91mm/段 8 5 239mm/段 7 14 21锯的次数少,损耗才少,所以要使损耗的铜管最少,锯得38毫米的铜管有7段,90毫米的铜管有8段。
1. 某大型体育馆,有一排长椅共45个座位,其中一些座位已经有人就座了。这时,又来了一个人要坐在这排长椅上,有趣的是,无论他坐在哪个座位上都会与已经就座的某个人相邻。原来至少有(
15
)人已经就座。(2分)
答案:
15
2. 观察下列每组算式。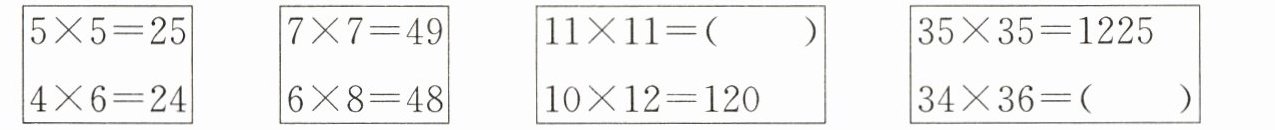
(1)在上面方框中的括号里写出得数。(2分)
(2)写出一组类似的算式:$\begin{array}{|l|}\hline ( ) \\\hline ( ) \\\hline\end{array}\\\hline $

(3)如果$a×a= m$($a$是不为0的自然数),那么$(a-1)×(a+1)= $( )。(1分)
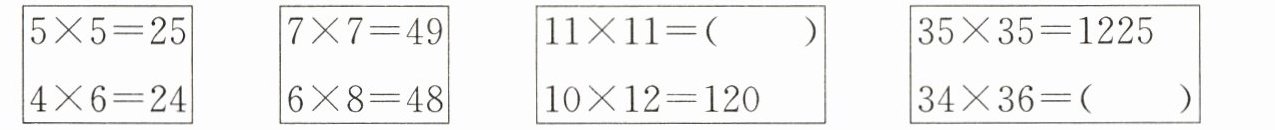
(1)在上面方框中的括号里写出得数。(2分)
121
1224
(2)写出一组类似的算式:$\begin{array}{|l|}\hline ( ) \\\hline ( ) \\\hline\end{array}\\\hline $
21×21=441
20×22=440
(2分)
(3)如果$a×a= m$($a$是不为0的自然数),那么$(a-1)×(a+1)= $( )。(1分)
m - 1
答案:
(1)121 1224 (2)21×21=441 20×22=440(答案不唯一) (3)m - 1
3. 某大型超市用大小相同的长方形木块铺地面,第1次铺2块,如图①;第2次把第1次铺的完全围起来,如图②;第3次把第2次铺的完全围起来,如图③……

(1)第5次铺完后,一共用去的木块数是(
(2)第$n$次铺完后,一共用去的木块数用含有字母$n$的式子可表示为(

(1)第5次铺完后,一共用去的木块数是(
90
)。(1分)(2)第$n$次铺完后,一共用去的木块数用含有字母$n$的式子可表示为(
2n(2n - 1)
)。(2分)
答案:
(1)90 (2)2n(2n - 1)
查看更多完整答案,请扫码查看


