《2025年初一入学分班测试卷七年级数学苏科版》

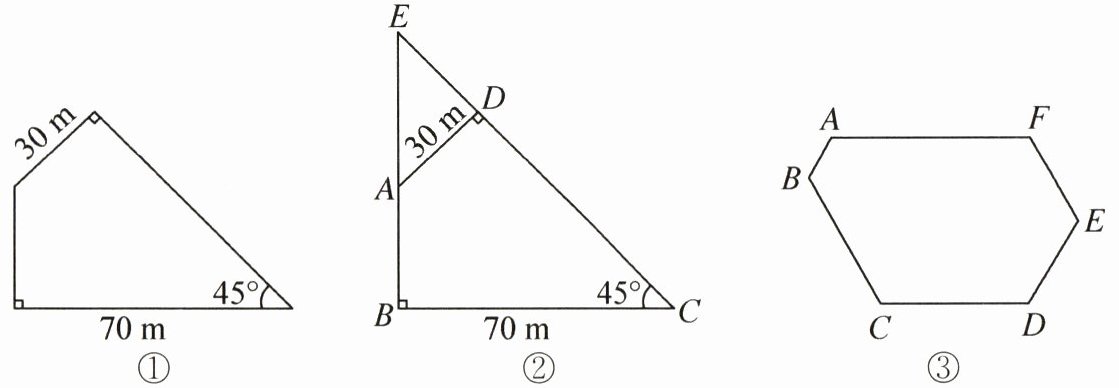
8. 数学课上,老师给同学们出了一道题,要大家求出一个四边形的面积(如图①)。奇奇一看,顿时就为难了,这是一个不规则的四边形啊！怎样计算它的面积呢？老师提示说：想想我们学过哪些平面图形的面积计算方法,能不能把它变成我们熟悉的图形计算它的面积呢？
奇奇灵光一闪,想到了一个好办法,他把四边形的两条边延长,使它们相交于点$E$(如图②)。他发现,因为$∠C= 45^{\circ}$,$∠B= 90^{\circ}$,所以$∠E= 45^{\circ}$,三角形$BCE$是一个等腰直角三角形,三角形$BCE的面积就是70×70÷2= 2450$(平方米)。又因为$∠ADE= 90^{\circ}$,$∠E= 45^{\circ}$,所以三角形$ADE$也是一个等腰直角三角形,它的面积是$30×30÷2= 450$(平方米),所以原来四边形的面积$=三角形BCE的面积-三角形ADE的面积= 2450-450= 2000$(平方米)。
奇奇解决问题的过程中,用到了转化的策略。
运用上面的策略,尝试解决下面的问题。
在六边形$ABCDEF$(如图③)中,六个角相等,均为$120^{\circ}$,$AB= 1$厘米,$BC= CD= 3$厘米,$DE= 2$厘米。这个六边形的周长是多少？(7分)

答案：
1 + 3 + 3 = 7(厘米)
7 - 3 - 2 = 2(厘米)
7 - 1 - 2 = 4(厘米)
1 + 3 + 3 + 2 + 2 + 4 = 15(厘米)
解析:如图，将六边形各边延长，使相交于点G、H、I,则三角形GHI是等边三角形,边长为1 + 3 + 3 = 7(厘米),进而求得EF与AF的长，即可得六边形的周长。