《2025年初一入学分班测试卷七年级数学苏科版》

4. 某校招生考试,报考学生有$\frac{1}{3}$被录取,被录取学生的平均分比录取分数线高6分,没被录取学生的平均分比录取分数线低24分,所有考生的平均分刚好为60分,那么录取分数线是多少分？(6分)

答案： 解:设录取分数线是x分，报考学生总数为a人。 $(x+6)×\frac{1}{3}a+(x-24)×(1-\frac{1}{3})a=60×a$ x=74

5. 如图①,在底面积为100平方厘米、高为20厘米的长方体水槽内放入一个长方体烧杯。以恒定不变的流速先向烧杯中注水,注满烧杯后,继续注水,直至注满水槽为止。此过程中,烧杯本身的质量、体积忽略不计,烧杯在大水槽中的位置始终不改变,水槽中水面上升的高度h(厘米)与注水时间t(秒)之间的关系如图②所示。

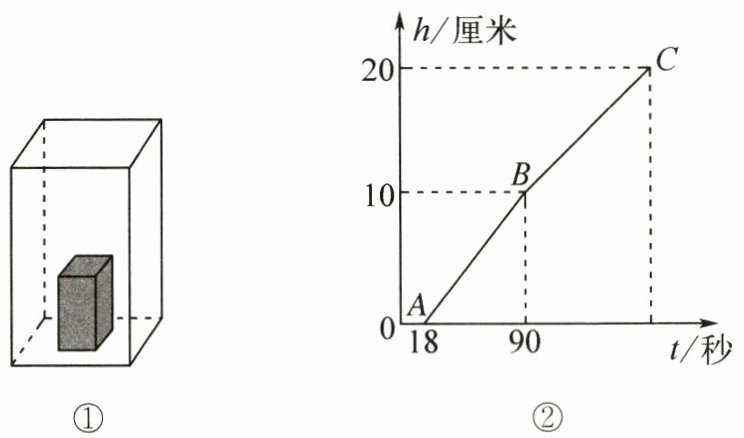
(1)图②中点(A)表示烧杯中刚好注满水,点(B)表示水槽中水面正好与烧杯中水面齐平。(2分)
(2)求烧杯的底面积。(2分)
解:设烧杯的底面积为x平方厘米。
$\frac{x}{100-x}=\frac{18}{90-18}$
x=20
(3)求注水的速度及注满空水槽所用的时间。(3分)
$20×10÷18=\frac{100}{9}$(立方厘米/秒)
$100×20÷\frac{100}{9}=180$(秒)

答案： （1）A B 解析:由图②可知，在0~18秒的时间里，水槽中水面的高度没有上升，即在这个时间里，一直是向烧杯中注水而没有向水槽里注水;从18秒开始水槽中水面开始上升，即此刻烧杯中刚注满水;在18~90秒的时间里，水槽中的水面高度以恒定不变的速度上升，而到90秒时，水槽中水面高度的上升速度减缓，说明此刻水面的高度已经与烧杯中的水面齐平。 （2）解:设烧杯的底面积为x平方厘米。 $\frac{x}{100-x}=\frac{18}{90-18}$ x=20 （3）$20×10÷18=\frac{100}{9}$(立方厘米/秒) $100×20÷\frac{100}{9}=180$(秒)