第33页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
1 [2025江苏南通质检]在没有电热毯等取暖设备的年代,人们用如图所示500mL的玻璃瓶装满开水放进被窝暖脚,睡觉前灌开水进去放被窝里,第二天早上还感觉温温的,水的比热容为$4.2×10^{3}J/(kg\cdot ^{\circ }C)$,这样一瓶水一夜放出的热量大约为(

A.$1.2×10^{3}J$
B.$1.2×10^{4}J$
C.$1.2×10^{5}J$
D.$1.2×10^{6}J$
C
)
A.$1.2×10^{3}J$
B.$1.2×10^{4}J$
C.$1.2×10^{5}J$
D.$1.2×10^{6}J$
答案:
C
质量为2kg的某物体温度从$20^{\circ }C升高到40^{\circ }C$时,吸收的热量为$1.84×10^{4}J$,则该物体的比热容为
$0.46× 10^3$
$J/(kg\cdot ^{\circ }C)$;若该物体的初始温度为$80^{\circ }C$,在放出相同的热量后,物体的温度会降低20
$^{\circ }C$(该物体的状态不发生变化)。
答案:
1. 首先求比热容$c$:
根据吸热公式$Q_{吸}=cm\Delta t$,其中$Q_{吸}=1.84×10^{4}J$,$m = 2kg$,$\Delta t=t - t_{0}=40^{\circ}C - 20^{\circ}C = 20^{\circ}C$。
由$c=\frac{Q_{吸}}{m\Delta t}$,将数值代入可得:
$c=\frac{1.84×10^{4}J}{2kg×20^{\circ}C}$。
计算$\frac{1.84×10^{4}}{2×20}=\frac{1.84×10^{4}}{40}=460$,所以$c = 460J/(kg\cdot^{\circ}C)$。
2. 然后求温度降低值$\Delta t'$:
已知$Q_{放}=Q_{吸}=1.84×10^{4}J$,$m = 2kg$,$c = 460J/(kg\cdot^{\circ}C)$,根据放热公式$Q_{放}=cm\Delta t'$。
则$\Delta t'=\frac{Q_{放}}{cm}$。
把$Q_{放}=1.84×10^{4}J$,$c = 460J/(kg\cdot^{\circ}C)$,$m = 2kg$代入可得:
$\Delta t'=\frac{1.84×10^{4}J}{460J/(kg\cdot^{\circ}C)×2kg}$。
先计算$460×2 = 920$,再计算$\frac{1.84×10^{4}}{920}=\frac{18400}{920}=20^{\circ}C$。
故答案依次为:$460$;$20$。
根据吸热公式$Q_{吸}=cm\Delta t$,其中$Q_{吸}=1.84×10^{4}J$,$m = 2kg$,$\Delta t=t - t_{0}=40^{\circ}C - 20^{\circ}C = 20^{\circ}C$。
由$c=\frac{Q_{吸}}{m\Delta t}$,将数值代入可得:
$c=\frac{1.84×10^{4}J}{2kg×20^{\circ}C}$。
计算$\frac{1.84×10^{4}}{2×20}=\frac{1.84×10^{4}}{40}=460$,所以$c = 460J/(kg\cdot^{\circ}C)$。
2. 然后求温度降低值$\Delta t'$:
已知$Q_{放}=Q_{吸}=1.84×10^{4}J$,$m = 2kg$,$c = 460J/(kg\cdot^{\circ}C)$,根据放热公式$Q_{放}=cm\Delta t'$。
则$\Delta t'=\frac{Q_{放}}{cm}$。
把$Q_{放}=1.84×10^{4}J$,$c = 460J/(kg\cdot^{\circ}C)$,$m = 2kg$代入可得:
$\Delta t'=\frac{1.84×10^{4}J}{460J/(kg\cdot^{\circ}C)×2kg}$。
先计算$460×2 = 920$,再计算$\frac{1.84×10^{4}}{920}=\frac{18400}{920}=20^{\circ}C$。
故答案依次为:$460$;$20$。
3 [2024安徽淮北期中]在实验室加热2kg的水,水的温度变化如图所示,已知水的比热容为$c_{水}= 4.2×10^{3}J/(kg\cdot ^{\circ }C)$,不计热量损失。
(1)在前3分钟加热的过程中,水吸收的热量是多少?
(2)若前3分钟水吸收的热量用于加热5kg的铝,可使铝的温度升高多少? [$c_{铝}= 0.84×10^{3}J/(kg\cdot ^{\circ }C)$]
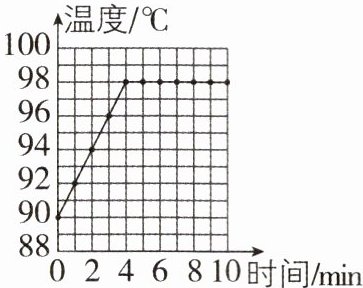
(1)在前3分钟加热的过程中,水吸收的热量是多少?
(2)若前3分钟水吸收的热量用于加热5kg的铝,可使铝的温度升高多少? [$c_{铝}= 0.84×10^{3}J/(kg\cdot ^{\circ }C)$]

答案:
(1)由图可知,前 3 分钟水升高的温度为$\Delta t=t - t_0=96\ ^\circ\text{C}-90\ ^\circ\text{C}=6\ ^\circ\text{C}$;前 3 分钟内水吸收的热量$Q_{\text{吸}}=c_{\text{水}}\ m\Delta t=4.2× 10^3\ \text{J/(kg}\cdot^\circ\text{C)}×2\ \text{kg}×6\ ^\circ\text{C}=5.04× 10^4\ \text{J}$。
(2)前 3 分钟水吸收的热量如果用于加热 5 kg 的铝,由于不计热量损失,则铝吸收的热量等于水吸收的热量,即$Q_{\text{铝吸}}=Q_{\text{吸}}$,则铝升高的温度为$\Delta t'=\frac{Q_{\text{铝吸}}}{c_{\text{铝}}m_{\text{铝}}}=\frac{5.04× 10^4\ \text{J}}{0.84× 10^3\ \text{J/(kg}\cdot^\circ\text{C)}×5\ \text{kg}}=12\ ^\circ\text{C}$。
(1)由图可知,前 3 分钟水升高的温度为$\Delta t=t - t_0=96\ ^\circ\text{C}-90\ ^\circ\text{C}=6\ ^\circ\text{C}$;前 3 分钟内水吸收的热量$Q_{\text{吸}}=c_{\text{水}}\ m\Delta t=4.2× 10^3\ \text{J/(kg}\cdot^\circ\text{C)}×2\ \text{kg}×6\ ^\circ\text{C}=5.04× 10^4\ \text{J}$。
(2)前 3 分钟水吸收的热量如果用于加热 5 kg 的铝,由于不计热量损失,则铝吸收的热量等于水吸收的热量,即$Q_{\text{铝吸}}=Q_{\text{吸}}$,则铝升高的温度为$\Delta t'=\frac{Q_{\text{铝吸}}}{c_{\text{铝}}m_{\text{铝}}}=\frac{5.04× 10^4\ \text{J}}{0.84× 10^3\ \text{J/(kg}\cdot^\circ\text{C)}×5\ \text{kg}}=12\ ^\circ\text{C}$。
4 [2025江苏连云港质检]甲、乙两种物质,质量之比是$3:2$,吸收相同的热量后,升高的温度之比是$2:3$,则甲、乙两种物质的比热容之比是(
A.$2:3$
B.$9:4$
C.$3:2$
D.$1:1$
D
)A.$2:3$
B.$9:4$
C.$3:2$
D.$1:1$
答案:
D
5 [2024湖北潜江质检]甲铁块的质量是乙铁块的3倍,吸收相同的热量,则甲、乙两铁块的比热容之比和升高的温度之比分别为(
A.$1:1;1:3$
B.$1:1;3:1$
C.$3:1;1:3$
D.$3:1;3:1$
A
)A.$1:1;1:3$
B.$1:1;3:1$
C.$3:1;1:3$
D.$3:1;3:1$
答案:
A
6 [2024四川成都质检]甲、乙两物体的质量之比为$2:1$,吸收的热量之比为$4:3$,它们升高的温度之比为$1:3$,则甲、乙两物体的比热容之比为
$2:1$
;若将甲物体使用一半,则剩下的部分比热容不变
(填“变大”“不变”或“变小”)。
答案:
$2:1$ 不变
7 [2025上海徐汇区期末,中]物理兴趣小组的同学在探究“沙子和水谁的吸热本领大”时,选用了两个完全相同的酒精灯,分别给质量都是200g的沙子和水加热。他们绘制出沙子和水的温度随加热时间变化的图像如图所示。已知水的比热容是$4.2×10^{3}J/(kg\cdot ^{\circ }C)$,求:
(1)加热2min时,水吸收的热量。
(2)沙子的比热容(结果保留1位有效数字)。
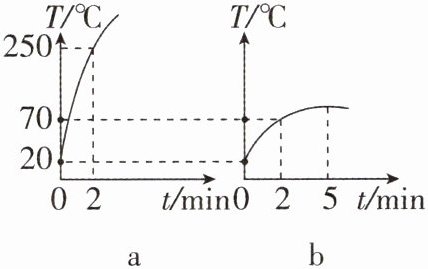
(1)加热2min时,水吸收的热量。
(2)沙子的比热容(结果保留1位有效数字)。

答案:
(1)由 b 图像可知,加热 2 min 时水的温度从$20\ ^\circ\text{C}$上升到$70\ ^\circ\text{C}$,水吸收的热量$Q_{\text{水吸}}=c_{\text{水}}m_{\text{水}}\Delta t_{\text{水}}=4.2× 10^3\ \text{J/(kg}\cdot^\circ\text{C)}×0.2\ \text{kg}×(70\ ^\circ\text{C}-20\ ^\circ\text{C})=4.2× 10^4\ \text{J}$。
(2)相同时间内完全相同的酒精灯燃烧放出相同的热量,在 2 分钟的时间内$Q_{\text{沙吸}}=Q_{\text{水吸}}=4.2× 10^4\ \text{J}$,又因为加热 2 min 时,沙子的温度从$20\ ^\circ\text{C}$上升到$250\ ^\circ\text{C}$,$\Delta t_{\text{沙}}=250\ ^\circ\text{C}-20\ ^\circ\text{C}=230\ ^\circ\text{C}$,$m_{\text{沙}}=200\ \text{g}=0.2\ \text{kg}$,$c_{\text{沙}}=\frac{Q_{\text{沙吸}}}{m_{\text{沙}}\Delta t_{\text{沙}}}=\frac{4.2× 10^4\ \text{J}}{0.2\ \text{kg}× 230\ ^\circ\text{C}}\approx0.9× 10^3\ \text{J/(kg}\cdot^\circ\text{C)}$。
(1)由 b 图像可知,加热 2 min 时水的温度从$20\ ^\circ\text{C}$上升到$70\ ^\circ\text{C}$,水吸收的热量$Q_{\text{水吸}}=c_{\text{水}}m_{\text{水}}\Delta t_{\text{水}}=4.2× 10^3\ \text{J/(kg}\cdot^\circ\text{C)}×0.2\ \text{kg}×(70\ ^\circ\text{C}-20\ ^\circ\text{C})=4.2× 10^4\ \text{J}$。
(2)相同时间内完全相同的酒精灯燃烧放出相同的热量,在 2 分钟的时间内$Q_{\text{沙吸}}=Q_{\text{水吸}}=4.2× 10^4\ \text{J}$,又因为加热 2 min 时,沙子的温度从$20\ ^\circ\text{C}$上升到$250\ ^\circ\text{C}$,$\Delta t_{\text{沙}}=250\ ^\circ\text{C}-20\ ^\circ\text{C}=230\ ^\circ\text{C}$,$m_{\text{沙}}=200\ \text{g}=0.2\ \text{kg}$,$c_{\text{沙}}=\frac{Q_{\text{沙吸}}}{m_{\text{沙}}\Delta t_{\text{沙}}}=\frac{4.2× 10^4\ \text{J}}{0.2\ \text{kg}× 230\ ^\circ\text{C}}\approx0.9× 10^3\ \text{J/(kg}\cdot^\circ\text{C)}$。
8 [中]在标准大气压下,将质量为2kg、初温为$25^{\circ }C$的水加热,当水吸收$6.72×10^{5}J$的热量后,水温会升高[$c_{水}= 4.2×10^{3}J/(kg\cdot ^{\circ }C)$](
A.$100^{\circ }C$
B.$75^{\circ }C$
C.$80^{\circ }C$
D.$105^{\circ }C$
B
)A.$100^{\circ }C$
B.$75^{\circ }C$
C.$80^{\circ }C$
D.$105^{\circ }C$
答案:
B
查看更多完整答案,请扫码查看


