《2025年初中必刷题九年级物理上册苏科版》

用如图装置提升物体,先将总重为G的两个钩码挂在均匀铁质杠杆上的A点,弹簧测力计作用于C点,竖直向上匀速拉动测力计,使钩码上升h,杠杆的机械效率为$η_1;$若仅将弹簧测力计改挂到B点,仍竖直向上匀速拉动测力计,使钩码上升h,杠杆的机械效率为$η_2,$不计其他阻力,则(B)

答案： B 【解析】原来弹簧测力计作用于C点，竖直向上匀速拉动弹簧测力计时，测得杠杆的机械效率为$η_{1}$；将弹簧测力计移动到B点时，仍将钩码竖直向上匀速提升相同的高度，根据$W_{有用}=Gh$可知有用功不变；钩码上升的高度相同，则杠杆重心上升的高度不变，根据$W_{额}=G_{杠杆}h_{杠杆}$可知，克服杠杆重力所做的额外功不变；由于有用功和额外功都不变，所以总功也不变，根据$η=\frac {W_{有用}}{W_{总}}×100\% $可知杠杆的机械效率不变，即$η_{1}=η_{2}$。

用如图所示的滑轮组拉着质量为2kg的物体A在水平桌面上做匀速直线运动。当拉力为5N时,物体A的速度为0.2m/s,滑轮组的机械效率为80%,下列说法正确的是(D)
A.绳子自由端移动的速度为0.4m/s
B.物体A受到的摩擦力为8N
C.拉力F的功率为2W
D.在物体A上放一重物后,滑轮组的机械效率将变大

答案： D 【解析】由图知$n=3$，绳子自由端移动的速度$v=nv_{物}=3×0.2m/s=0.6m/s$，故A错误；使用滑轮组水平拉动物体做匀速直线运动时，克服物体与桌面间的摩擦力所做的功为有用功，绳子自由端拉力做的功为总功，由$η=\frac {W_{有用}}{W_{总}}×100\% =\frac {fs_{物}}{Fs}×100\% =\frac {f}{nF}×100\% $可得，物体受到的摩擦力$f=ηnF=80\% ×3×5N=12N$，故B错误；拉力的功率$P=\frac {W_{总}}{t}=\frac {Fs}{t}=Fv=5N×0.6m/s=3W$，故C错误；在物体A上放一重物后，接触面的粗糙程度不变，压力变大，所以A与桌面间的摩擦力变大，物体A通过相同距离时，有用功变大，但额外功几乎不变，由$η=\frac {W_{有用}}{W_{总}}×100\% =\frac {W_{有用}}{W_{有用}+W_{额}}×100\% $可知，滑轮组的机械效率将变大，故D正确。

电梯是高层住宅必备的工具。如图是某种升降电梯的工作原理图,它由轿厢M,配重m,电动机,钢丝绳,定滑轮A、B,动滑轮C等部件连接组成,电梯的最大载重量指的是除空轿厢质量外能承载的最大质量。配重的质量m配= 1200kg(配重看成整个系统动力的一部分),空轿厢的质量为1000kg,动滑轮C的质量为100kg,电动机的最大功率为43.5kW,电梯在运行过程中总是以1.5m/s的速度做匀速直线运动。若某次电梯向上运动,载人后轿厢与人的总质量为3900kg。不计一切摩擦和绳重,g取10N/kg,则以下结论正确的是(D)
A.电动机此时的拉力大小为$2×10^4N$
B.电动机此时的功率为$2.1×10^4W$
C.该电梯的最大载重量为4000kg
D.该电梯此时的机械效率为72.5%

答案： D 【解析】整个装置中，配重拉着动滑轮的轴，有三段绳子承担着动滑轮与轿厢及其中的人的总重，则有$2F_{拉}+G_{配}=G_{总}$，电动机此时的拉力大小为$F_{拉}=\frac {G_{总}-G_{配}}{2}=\frac {(m_{总}+m_{动}-m_{配})g}{2}=\frac {(3900kg+100kg-1200kg)×10N/kg}{2}=1.4×10^{4}N$，故A错误。由图可知，电动机所拉绳子移动的速度$v_{绳}=nv_{厢}=2×1.5m/s=3m/s$，由$P=\frac {W}{t}=\frac {Fs}{t}=Fv$可知，电动机此时的功率为$P=F_{拉}v_{绳}=1.4×10^{4}N×3m/s=4.2×10^{4}W$，故B错误。电动机的最大功率为43.5kW，电动机所拉绳子移动的速度一定，为3m/s，根据$P=\frac {W}{t}=\frac {Fs}{t}=Fv$可知，电动机对绳子的最大拉力为$F_{大}=\frac {P_{大}}{v_{绳}}=\frac {43.5×10^{3}W}{3m/s}=1.45×10^{4}N$，能提升的最大总重为$G'_{总}=2F_{大}+m_{配}g=2×1.45×10^{4}N+1200kg×10N/kg=4.1×10^{4}N$，该电梯的最大载重量为$m_{大}=\frac {G'_{总}-G_{厢}-G_{动}}{g}=\frac {G'_{总}}{g}-m_{厢}-m_{动}=\frac {4.1×10^{4}N}{10N/kg}-1000kg-100kg=3000kg$，故C错误。电梯向上运动，载人后轿厢与人的总质量为3900kg，人的总质量$m_{人}=m_{总}-m_{厢}=3900kg-1000kg=2900kg$，该电梯此时的机械效率为$η=\frac {W_{有用}}{W_{总}}×100\% =\frac {m_{人}gh}{m_{配}gh+F_{拉}×2h}×100\% =\frac {2900kg×10N/kg×h}{1200kg×10N/kg×h+1.4×10^{4}N×2h}×100\% =72.5\% $，故D正确。

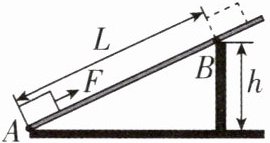
4[2023四川泸州中考,中]小聪探究斜面的机械效率时,将粗糙程度均匀的长木板用支架支撑构成斜面,如图所示。用刻度尺量出斜面底端A点到斜面上B点的距离L为80cm,B点距水平地面高度h为20cm。沿斜面向上用0.8N的拉力F将重为2N的木块匀速拉到B点,用时2s,则这段过程中拉力F做功的功率P= ______W,斜面的机械效率η= ______%,木块在该斜面上受到的滑动摩擦力f= ______N。

0.3262.50.3

答案： 0.32 62.5 0.3【解析】拉力做的总功$W_{总}=FL=0.8N×0.8m=0.64J$，拉力做功的功率$P=\frac {W_{总}}{t}=\frac {0.64J}{2s}=0.32W$；拉力做的有用功$W_{有用}=Gh=2N×0.2m=0.4J$，斜面的机械效率$η=\frac {W_{有用}}{W_{总}}×100\% =\frac {0.4J}{0.64J}×100\% =62.5\% $；克服滑动摩擦力做的额外功$W_{额}=W_{总}-W_{有用}=0.64J-0.4J=0.24J$，由$W_{额}=fL$可得木块受到的滑动摩擦力$f=\frac {W_{额}}{L}=\frac {0.24J}{0.8m}=0.3N$。

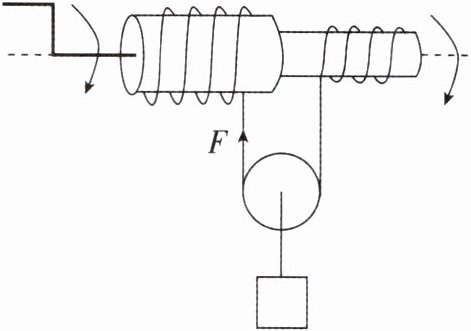
5[2025山东青岛期末,中]如图所示的机械装置,由一个动滑轮和带有摇把的两个圆柱体组成,两个圆柱体圆形截面的直径不同,两个圆柱体和摇把固定在同一转轴上,一根粗细均匀的轻绳绕过动滑轮紧密缠绕在两圆柱体上,轻绳的两端分别固定在两个圆柱体两端。当摇把以如图所示的方向匀速转动时,重物被提起。已知摇把每秒转r圈,重物重力为G,大圆柱体和小圆柱体圆形截面的半径分别为$R_1$和$R_2,$滑轮的机械效率为η,忽略所有接触面之间的摩擦。求:
(1)图中绳的拉力F的大小。
(2)摇把转动一圈,重物上升的高度。
(3)机械对重物的拉力做功的功率。

答案： 【解】
(1)由图可知，$n=2$，根据$η=\frac {W_{有用}}{W_{总}}×100\% =\frac {Gh}{Fs}×100\% =\frac {Gh}{Fnh}×100\% $可知，绳的拉力F的大小为$F=\frac {G}{2η}$。
(2)摇把旋转一周时，大圆柱体和小圆柱体各转一周，靠近小圆柱体一侧绳子下降，靠近大圆柱体一侧绳子上升，此时重物上升的高度$h=\frac {2πR_{1}-2πR_{2}}{2}=π(R_{1}-R_{2})$。
(3)摇把每秒转r圈，则重物每秒上升的高度$h'=rh=rπ(R_{1}-R_{2})$，机械对重物的拉力做的功为$W_{拉}=G×h'=G×rπ(R_{1}-R_{2})=rπG(R_{1}-R_{2})$，机械对重物的拉力做功的功率为$P=\frac {W_{拉}}{t}=\frac {rπG(R_{1}-R_{2})}{1s}=rπG(R_{1}-R_{2})$。