《2025年一遍过八年级数学上册人教版》

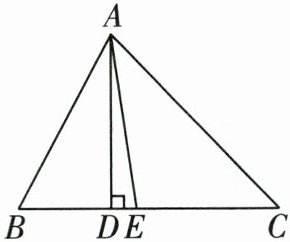
1 如图,AD 是△ABC 的高,AE 平分∠BAC,交 BC 于点 E.
(1)若∠B = 62°,∠C = 46°,求∠DAE 的度数；
(2)若∠B - ∠C = 30°,求∠DAE 的度数.

答案： 1 解:
(1)
∵AD是△ABC的高,∠B=62°,∠C=46°,
∴∠BAC=180° - ∠B - ∠C=72°,∠BAD=90° - ∠B=28°.
∵AE平分∠BAC,
∴∠BAE= $\frac{1}{2}$∠BAC=36°,
∴∠DAE=∠BAE - ∠BAD=8°.
(2)
∵∠B - ∠C=30°,
∴∠B=∠C + 30°,
∴∠BAC=180° - ∠B - ∠C=150° - 2∠C,
∵AD是△ABC的高,
∴∠BAD=90° - ∠B=60° - ∠C.
∵AE平分∠BAC,
∴∠BAE= $\frac{1}{2}$∠BAC=75° - ∠C,
∴∠DAE=∠BAE - ∠BAD=75° - ∠C - (60° - ∠C)=15°.

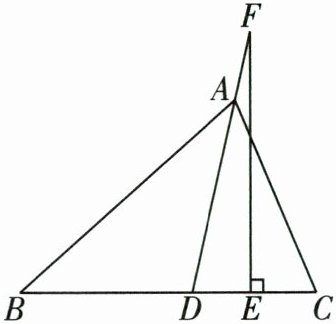
2 如图,在△ABC 中,AD 平分∠BAC,交 BC 于点 D,点 F 在 DA 的延长线上,FE⊥BC 于点 E,∠B = α,∠C = β(α ＜ β),请用含α,β的代数式表示∠DFE.

答案： 2 解:
∵∠B=α,∠C=β,
∴∠BAC=180° - α - β.
∵AD平分∠BAC,
∴∠CAD= $\frac{1}{2}$∠BAC=90° - $\frac{1}{2}$(α + β),
∴∠ADE=180° - ∠C - ∠CAD=90° + $\frac{1}{2}$(α - β).
∵FE⊥BC,
∴∠FED=90°,
∴∠DFE=90° - ∠ADE= $\frac{1}{2}$(β - α).

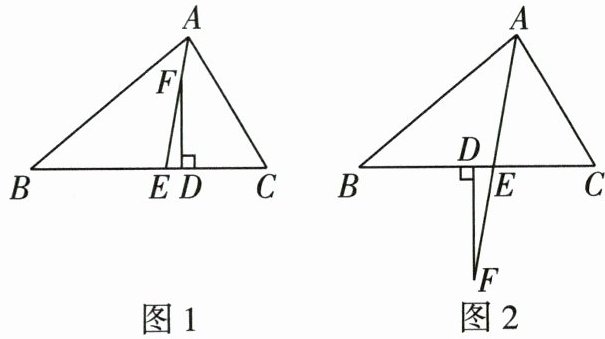
3 如图,在△ABC 中,AE 平分∠BAC,交 BC 于点 E,F 为直线 AE 上一点,且 FD⊥BC 于点 D.(∠C ＞ ∠B)
(1)如图 1,若∠B = 40°,∠C = 60°,点 F 在线段 AE 上,求∠EFD 的度数；
(2)如图 2,当点 F 在 AE 的延长线上时,请猜想∠EFD 与∠B,∠C 之间的数量关系,并加以证明.

答案： 3 解:
(1)
∵∠B=40°,∠C=60°,
∴∠BAC=80°.
∵AE平分∠BAC,
∴∠CAE= $\frac{1}{2}$∠BAC=40°,
∴∠FEC=180° - ∠C - ∠CAE=80°.
∵FD⊥BC,
∴∠FDE=90°,
∴∠EFD=90° - ∠FEC=10°.
(2)∠EFD= $\frac{1}{2}$(∠C - ∠B).证明如下:
∵AE平分∠BAC,
∴∠BAE= $\frac{1}{2}$∠BAC= $\frac{1}{2}$(180° - ∠B - ∠C)=90° - $\frac{1}{2}$(∠B + ∠C),
∴∠AEB=180° - ∠B - ∠BAE=90° + $\frac{1}{2}$(∠C - ∠B),
∴∠FED=180° - ∠AEB=90° + $\frac{1}{2}$(∠B - ∠C).
∵FD⊥BC,
∴∠FDE=90°,
∴∠EFD=90° - ∠FED= $\frac{1}{2}$(∠C - ∠B).

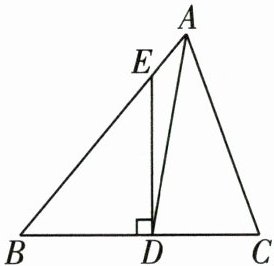
4 如图,在△ABC 中,AD 是△ABC 的角平分线,过点 D 作 DE⊥BC,交 AB 于点 E.
(1)若∠B = 50°,∠C = 70°,求∠ADE 的度数；
(2)若∠B = α,∠C = β(β ＞ α),则∠ADE 的度数为______(用含α,β的式子表示).

答案： 4 解:
(1)
∵∠B=50°,∠C=70°,
∴∠BAC=180° - ∠B - ∠C=60°.
∵AD是△ABC的角平分线,
∴∠BAD= $\frac{1}{2}$∠BAC=30°,
∴∠BDA=180° - ∠B - ∠BAD=180° - 50° - 30°=100°.
∵DE⊥BC,
∴∠BDE=90°,
∴∠ADE=∠BDA - ∠BDE=10°.
(2) $\frac{1}{2}$(β - α)
解法提示:
∵∠BAC=180° - ∠B - ∠C,AD是△ABC的角平分线,
∴∠BAD= $\frac{1}{2}$∠BAC= $\frac{1}{2}$(180° - ∠B - ∠C)=90° - $\frac{1}{2}$∠B - $\frac{1}{2}$∠C,
∴∠BDA=180° - ∠B - ∠BAD=180° - ∠B - (90° - $\frac{1}{2}$∠B - $\frac{1}{2}$∠C)=90° + $\frac{1}{2}$∠C - $\frac{1}{2}$∠B.
∵DE⊥BC,
∴∠BDE=90°,
∴∠ADE=∠BDA - ∠BDE=(90° + $\frac{1}{2}$∠C - $\frac{1}{2}$∠B) - 90°= $\frac{1}{2}$(∠C - ∠B)= $\frac{1}{2}$(β - α).